Расчёт частоты электрического сигнала

Для некоторых функций релейной защиты и автоматики необходима информация о частоте наблюдаемого напряжения или тока. В дополнение к ранее опубликованной статье, в которой были приведены наиболее оптимальные сигналы, по которым следует рассчитывать частоту сети, рассмотрим вариант расчёта частоты электрического сигнала по переходу через ноль.

Рассмотрим синусоидальный сигнал, например, напряжения сети (рис. 1). На рисунке отмечен период сигнала T. Частота f является величиной, обратной периоду, т.е. f = 1 / T.

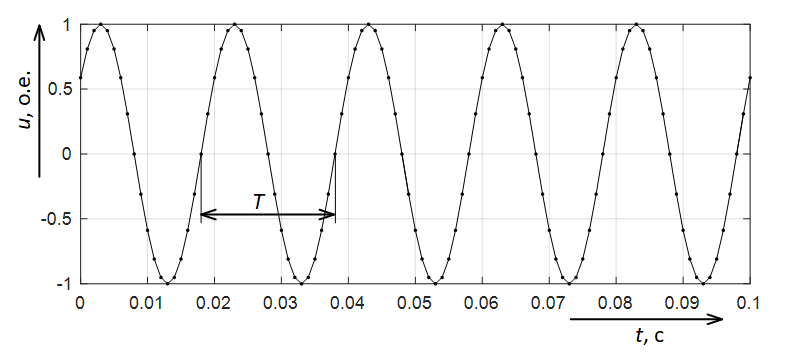
Рис. 1. Пример синусоидального сигнала

Таким образом, для того, чтобы определить частоту сигнала, необходимо рассчитать его период. В идеальном случае для этого достаточно определить соседние моменты времени, в которых наблюдаемый сигнал переходит нулевое значение в одном и том же направлении (например, из области отрицательных значений в область положительных значений сигнала). Однако в цифровой релейной защите наблюдаемые сигналы дискретизированы (т.е. значения наблюдаемого сигнала фиксируются в определённые дискретные моменты времени с определённой частотой дискретизации f_д через равные промежутки времени τ, называемые интервалом дискретизации), в связи с чем возникает проблема определения момента перехода через ноль.

В качестве возможного решения указанной проблемы применяется линейная интерполяция наблюдаемого сигнала в те моменты времени, в которые исследуемый сигнал не регистрируется. На рис. 2 показана иллюстрация данного подхода.

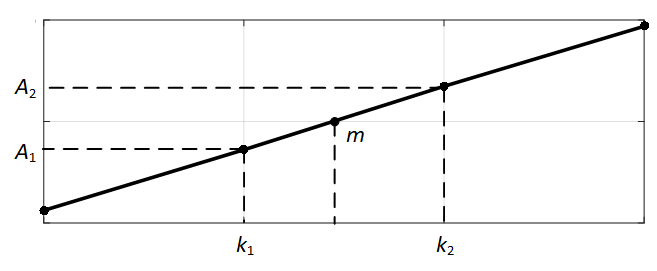
Рис. 2. Линейная интерполяция дискретизированного сигнала

Составим алгоритм определения расчётного момента времени перехода через ноль сигнала (по рисунку 2):

1. Определяем дискретный момент времени k₂, когда наблюдаемый сигнал переходит из области отрицательных значений в области положительных значений (или наоборот).
2. Фиксируем значения сигнала A₁ и A₂ в дискретные моменты времени k₁ и k₂ соответственно.
3. Рассчитываем значение m исходя из уравнения прямой, проходящей через 2 точки.

Учитывая, что (k₂ – k₁) = 1, значение m определяется по следующему выражению:

$$ m = \frac{\lvert A_1 \rvert}{\lvert A_1 \rvert + A_2} $$

После определения соседних моментов времени перехода через ноль рассчитывается период сигнала. Рассмотрим сигнал по рис. 3.

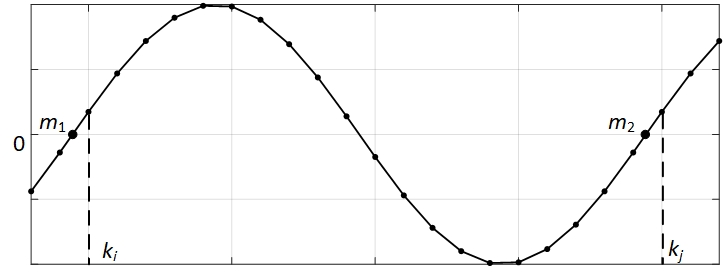
Рис. 3. Рассматриваемый сигнал

Для данного сигнала с принятыми обозначениями период сигнала будет определяться по следующему выражению

$$ T = (k_j + m_2- k_i- m_1) \cdot \tau, $$

где $ \tau $ — интервал дискретизации сигнала.

После появления очередного перехода через производится перерасчёт частоты в соответствии с указанным выше алгоритмом. Приведённый в статье алгоритм расчёта частоты по переходу через ноль приведён в приложенном файле программы в среде Matlab: freq_calc.m.

На рис. 4 приведен результат расчёта частоты модельного сигнала, содержащего переходный процесс.

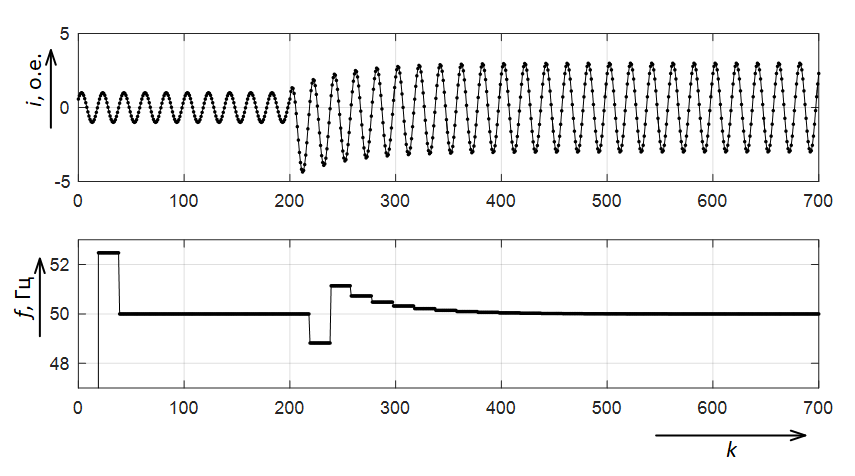
Рис. 4. Исходный сигнал и результаты расчёта частоты данного сигнала

Из результатов видно, что расчёт частоты по переходу через ноль обладает большой погрешностью в переходном режиме. Для уменьшения данной погрешности, к примеру, используют усреднение значения на нескольких периодах.