Consider the effect of the window Fourier transform on the operation of distance protection.
Measurement of distance protection – complex resistance. The complex resistance is calculated from the complexes of voltages and currents, which, as a rule, are isolated using the so-called two-half-period (period) Fourier filter. This Fourier filter is nothing more than a Fourier transform with an observation window during the period of the nominal network frequency (20 ms). In this case, the window is rectangular.
Also consider the same Fourier filter, but with a window. Let it be a Hamming window (Fig. 1).
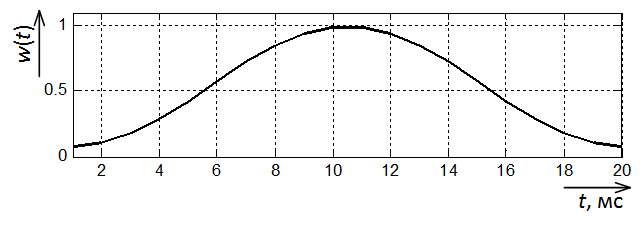Fig. 1. Hamming window
Remote protection responds to short circuits, so we will check the operation of these two filters during a short circuit. In this case, we restrict ourselves only to current (probably, while this will be enough, if necessary, we will also attract voltage).
First, take a current signal without an aperiodic component of the transient process (Fig. 2).
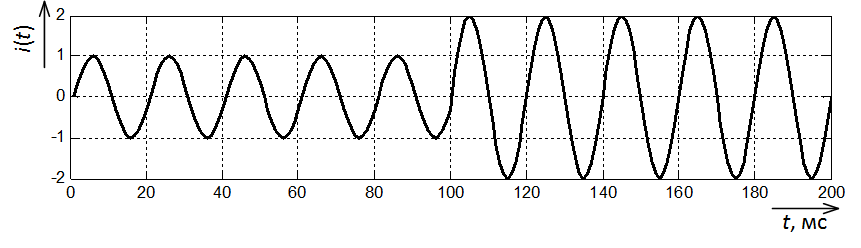
Fig. 2. Oscillogram of the short-circuit current without an aperiodic component
The results of a simple Fourier filter, without a window, are shown in Fig. 3.
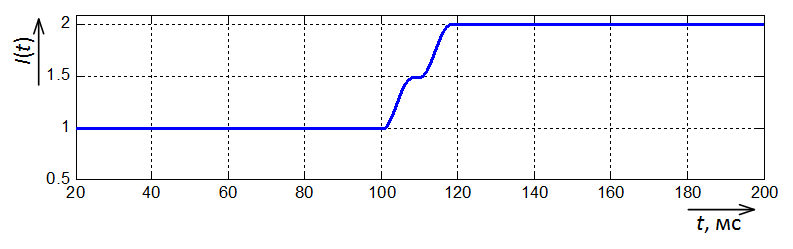Fig. 3. Oscillogram of current amplitude at the output of a simple Fourier filter
The results of the Fourier filter with the Hamming window are shown in Fig. 4.
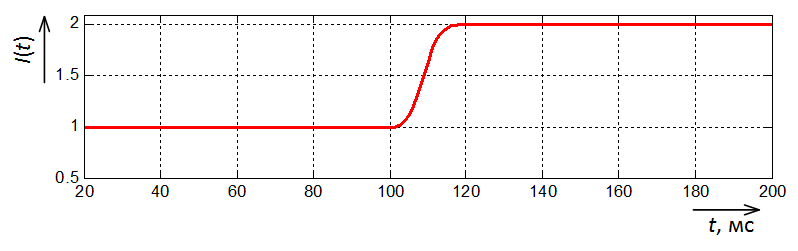
Fig. 4. Oscillogram of the amplitude of the current at the output of the Fourier filter with a Hamming window
What did we get? Apart from the transient in the filters, the results are completely identical.
Next, we take a current signal containing the aperiodic component of the transient process (Fig. 5).
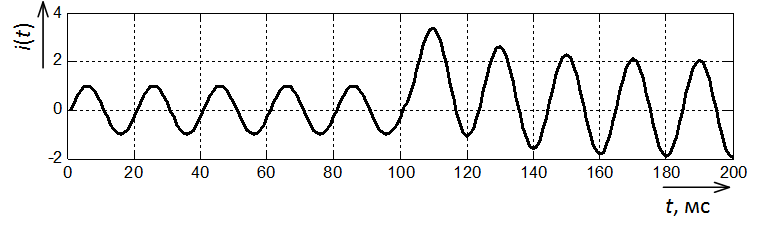
Fig. 5. Oscillogram of a short-circuit current with an aperiodic component
In fig. 6 together shows the results of a simple Fourier filter (blue) and a Fourier filter with a Hamming window (red).
Fig. 6. Oscillogram of current amplitude at the output of a simple Fourier filter and a Fourier filter with a Hamming window
ВIt is obvious that Fourier with the Hamming window has rather decent fluctuations, much more than a simple Fourier. Why is that? Let’s get it right.
Let’s look at the amplitude-frequency characteristics of both filters (Fig. 7).
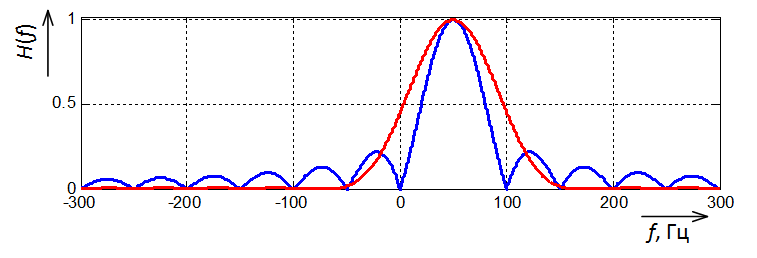
Fig. 7. Frequency response (AFC) of a simple Fourier filter (blue) and a Fourier filter with a Hamming window (red)
Firstly, we notice that a Fourier filter with a window gives much smaller side lobes compared to a simple Fourier filter. This is his plus. But what does this have to do with the vibrations we find coming from the aperiodic component? Obviously not.
Secondly, we see that the main lobe of the frequency response of a window Fourier is wider than that of a simple Fourier. This means that it has worse frequency resolution. In other words, a Fourier filter with a window distinguishes between close frequencies worse; they seem to mix with each other. In our case, two fairly close frequencies are important. It is 50 Hz and 0 Hz. In a simple Fourier filter, 0 Hz is not mixed at all at 50 Hz, i.e. 100% inhibited. What can not be said about Fourier with a window. The component of 0 Hz is suppressed only by 50%. Now recall that aperiodic is a component with a frequency of 0 Hz … So there was a reason for the large fluctuations in the output of the filter with the window Fourier.
So, the window Fourier transform is not very suitable for the implementation of conventional measuring bodies of relay protection, in particular, a resistance relay. It is better to use a regular Fourier filter (well, or something completely different).