In the study of electrical circuits and modeling, vector diagrams of currents and voltages are often used. Under the vector diagram refers to a set of vectors depicting sinusoidal functions of time [1].
- Representation of sinusoidal functions as complex numbers
- Ohm’s law in complex form
- Vector diagram with serial connection of elements
- Vector diagram with parallel connection of elements
Representation of sinusoidal functions as complex numbers
The vector diagram is a convenient tool for representing the sinusoidal functions of time, which, for example, are the voltages and currents of an alternating current circuit.
Consider, for example, an arbitrary current represented as a sinusoidal function
i(t) = 10 sin(ωt + 30°).
This sinusoidal signal can be represented as a complex quantity
I = 10∠30°.

To form a complex number, the module and phase of the sinusoidal signal are used.
Ohm’s law in complex form
It is known [1] that the voltage U on the resistance Z is connected with the current I flowing through this resistance, according to Ohm’s law:
U = Z ∙ I.
In addition, the relations are known that determine the resistance of a resistor, the inductance of a coil and the capacitance of a capacitor:
ZR = R, ZL = jXL, ZC = −jXC,
where XL = ωL, XC = 1/(ωC), R – resistor resistance, L – coil inductance, C – capacitor capacity, ω = 2pf – cyclic frequency, f – network frequency, j – imaginary unit.
Vector diagram with serial connection of elements
To construct vector diagrams, first, they compose equations according to Kirchhoff’s laws for the electrical circuit in question.
Consider the electrical circuit shown in Fig. 1, and draw a vector diagram of stresses for it. Denote the voltage drop across the elements.
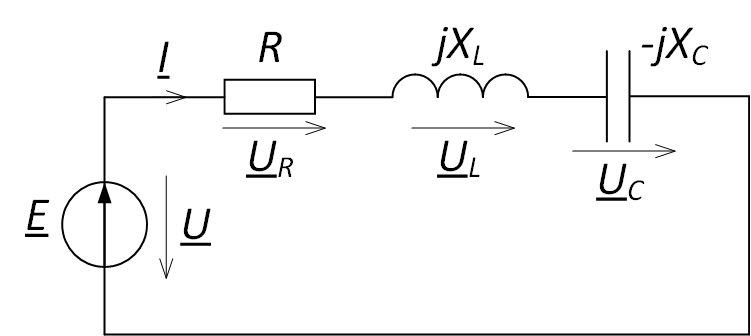 Fig. 1. Series connection of circuit elements
Fig. 1. Series connection of circuit elements
We compose the equation for this circuit according to the second law of Kirchhoff:
UR + UL + UC = E.
According to Ohm’s law, the voltage drop across the elements is determined by the following expressions:
UR = I ∙ R,
UL = I ∙ jXL,
UC = −I ∙ jXC.
To build a vector diagram, it is necessary to display the terms given in the equation on the complex plane. Typically, the current and voltage vectors are displayed on their scales: separately for voltages and separately for currents.
It is known from the course of mathematics that j = 1∠90°, −j = 1∠ − 90°. Hence, when constructing a vector diagram, multiplying a vector by an imaginary unit j leads to a rotation of this vector 90 degrees counterclockwise, and multiplying by −j leads to a rotation of this vector 90 degrees clockwise.
When constructing a vector diagram of stresses on the complex plane, we first display the current vector I, and then we will display the relative vector of voltage drops (Fig. 2), taking into account the above relations for the imaginary unit.
The voltage drop across the resistor UR coincides with the current I (since UR = I ∙ R, and R is a purely real quantity or, in simple words, there is no multiplication by an imaginary unit). The voltage drop across the inductive reactance is ahead of the current vector by 90° (since UL = I ∙ jXL, and multiplying by j causes this vector to rotate 90° counterclockwise). The voltage drop across the capacitance is 90° behind the current vector (because UC = −I ∙ jXC, and multiplying by −j rotates this vector 90° clockwise).

Fig. 2. Vector diagram of stresses in series connection of circuit elements
It should be noted that only vectors of those quantities for which the frequency coincides are shown on one vector diagram!
Vector diagram with parallel connection of elements
Consider the electrical circuit shown in Fig. 3, and draw a vector diagram of the currents for it. Immediately denote the direction of the currents in the branches.

Рис. 3. Параллельное соединение элементов цепи
We compose the equation for this circuit according to the first law of Kirchhoff:
I – IR – IL – IC = 0,
where from
I = IR + IL + IC.
According to Ohm’s law, we determine the currents in the branches by the following expressions, given that 1 / j = −j:
IR = E / R,
IL = E / (jXL) = −j ∙ E / XL,
IC = E / (−jXC) = j ∙ E / XC,
To build a vector diagram, it is necessary to display the terms given in the equation on the complex plane.
When constructing a vector diagram of currents on the complex plane, we first display the EMF vector E, after which we will display the current vector of currents (Fig. 4) taking into account the above relations for the imaginary unit.
The current in the resistor IR coincides in direction with the EMF E (since IR = E / R, and R is a purely real quantity or, in simple words, there is no multiplication by an imaginary unit). The current in the inductive reactance is 90° behind the EMF vector (since IL = −j ∙ E / XL, and multiplying by −j causes this vector to rotate 90° clockwise). The current in capacitance is ahead of the EMF vector by 90° (since IC = j ∙ E / XC, and multiplying by j causes this vector to rotate 90° counterclockwise). The resulting current vector is determined after the geometric addition of all vectors according to the parallelogram rule.
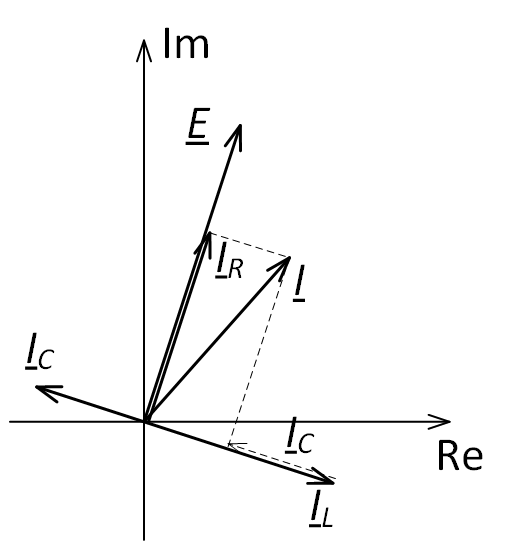
Fig. 4. Vector diagram of currents with parallel connection of circuit elements
For an arbitrary circuit, the algorithm for constructing vector diagrams is similar to the above, taking into account the currents and applied voltages flowing in the branches.
Please note that the site provides a tool for building vector diagrams online for three-phase circuits.
References
- Zeveke G.V., Ionkin P.A., Netushil A.V., Strakhov S.V. Osnovy teorii tsepey. Uchebnik dlya vuzov. Izd. 4-ye, pererabotannoye. M., «Energiya», 1975.