Суть преобразования Фурье

Содержание данной заметки раскрывает вопросы как и почему работает известное всем энергетикам преобразование Фурье. Здесь мы постарались воздержаться от использования сложного понятийного аппарата, все использованные выкладки должны быть понятны каждому, кто хоть как-то овладел начальным уровнем университетского курса высшей математики. Для всех остальных не исключено понимание изложенного материала на интуитивном уровне.

В настоящее время преобразование Фурье широко используется как основа различных инструментов анализа аварийных осциллограмм. Примеры его использования в современных программах просмотра осциллограмм:

• выделение действующего значения записанной электрической величины и её текущей фазы (рис. 1);
• получение спектра – рис. 2;
• построение векторной диаграммы (рис. 3);
• построение временных годографов комплексных замеров электрических величин (к примеру, сопротивлений) – рис. 4.

Рис. 1. Иллюстрация применения преобразования Фурье для выделения действующего значения тока

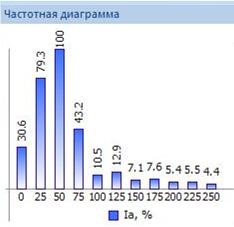Рис. 2. Спектр как пример использования преобразования Фурье

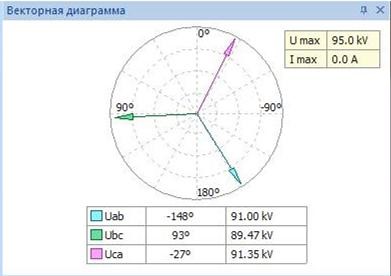
Рис. 3. Векторная диаграмма как пример использования преобразования Фурье

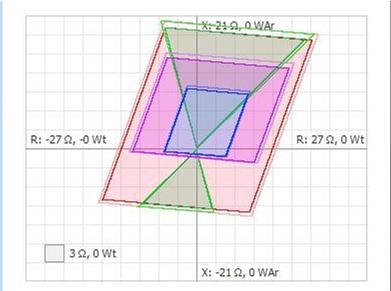
Рис. 4. Годограф сопротивления как пример использования преобразования Фурье

Таким образом, роль преобразования Фурье в анализе аварийных осциллограмм сложно переоценить. Далее перейдём к его сути.

1. Преобразование Фурье – это некий линейный оператор (см. рис. 5), который преобразует входной сигнал u(t) во временной области (t – это время) в сигнал U(f) в частотной области (f – это частота).

Рис. 5. Преобразование Фурье как «чёрный ящик»

2. Предполагается, что входной сигнал u(t) состоит из набора (суммы) косинусоид следующего вида:

,

где f – частота; A – амплитуда; φ₀ – начальная фаза.

Далее идёт очень важное утверждение. В соответствии с  известной формулой Эйлера, функция cos определяется как  сумма двух комплексных экспонент:

,

где  – мнимая единица.

Теперь можно внести уточнение: в общем случае преобразование Фурье предполагает, что входной сигнал u(t) состоит не из набора косинусоид, как это утверждалось чуть выше, а из  набора комплексных экспонент.

Примечание: в преобразовании Фурье частота f – это частота комплексной экспоненты, а не косинусоиды.

Рассмотрим подробнее, из каких именно комплексных экспонент состоит косинусоида s(t). Первая экспонента e₁(t) описывает на комплексной плоскости равномерное движение точки по окружности с радиусом A/2 с постоянной угловой скоростью ω = 2πf – см. рис. 6.

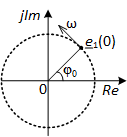
Рис. 6. Первая комплексная экспонента, из которой состоит косинусоида

Вторая экспонента e₂(t) – это сестра-близнец первой экспоненты e₁(t), но в отличие от неё она описывает вращение точки по окружности в противоположную сторону – см. рис. 7. Также заметим, что графики e₁(t) и e₂(t) симметричны относительно действительной оси Re.

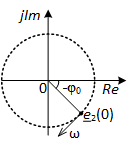Рис. 7. Вторая комплексная экспонента, из которой состоит косинусоида

Итак, косинусоида с частотой f состоит из комплексной экспоненты с частотой f и комплексной экспоненты с частотой —f.

3. Такие периодические функции как синусоида, косинусоида и комплексная экспонента обладают очень важным с точки зрения преобразования Фурье свойством: их среднее значение (и интеграл тоже) на периоде равен нулю. Иными словами, если взять комплексную экспоненту с частотой f_x и усреднить её на периоде 1/f_x, то в результате усреднения мы получим нулевое значение. Это правило справедливо практически для всех комплексных экспонент с любой частотой f_x. Но в этом правиле есть одно исключение. Это экспонента с частотой f = 0 Гц, т.е. постоянная составляющая. В результате усреднения постоянной составляющей на любом интервале времени получается сама постоянная составляющая, т.е. она не обнуляется.

Посмотрим, как на рассмотренном правиле построено преобразование Фурье.

В качестве примера возьмём косинусоиду с частотой 50 Гц и амплитудой A. Мы знаем, что эта косинусоида состоит из двух комплексных экспонент с частотами -50 Гц и +50 Гц. Как эти составляющие расположены в области частот можно увидеть на рис. 8. Всего лишь два значения |U(f)| ненулевые ­– в точках -50 Гц и +50 Гц.

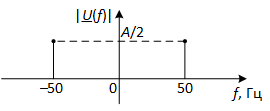
Рис. 8. Вид косинусоиды с частотой 50 Гц и амплитудой A в области частот

Если преобразование Фурье предназначено для преобразования сигнала во временной области u(t) в сигнал в частотной области U(f), то в случае косинусоиды u(t)=s(t) в качестве U(f) мы должны получить функцию, изображённую на рис. 8. Что такого можно сделать с s(t), чтобы на выходе получить |U(f)| как на рис. 8? Для простоты ограничимся не всей функцией |U(f)|, а только лишь одним её значением в точке f=50 Гц. В этой точке значение функции должно быть |U(50)|=A/2.

Итак, нам дана косинусоида s(t), заданное значение частоты f=50 Гц и информация о том, что при этой частоте должно выполняться равенство |U(50)|=A/2. Как нужно преобразовать s(t), чтобы на выходе преобразования было |U(50)|=A/2? Очевидно, что если просто усреднить косинусоиду s(t) на периоде 1/f=1/50=0,02 с, то на выходе мы получим ноль, т.е. |U(50)|=0. Поэтому просто усреднение на периоде не годится в качестве искомого преобразования. Попробуем другой вариант. Умножим s(t) на комплексную экспоненту с частотой -50 Гц:

.

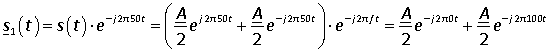В результате входящая в состав косинусоиды s(t) экспонента с частотой ­-50 Гц превратилась в экспоненту с частотой -100 Гц, а экспонента с частотой +50 Гц превратилась в комплексную экспоненту с частотой 0 Гц, т.е. в постоянную составляющую. Налицо смещение частот всех комплексных экспонент, входящих в состав входного сигнала, на значение -50 Гц. То, как после этого стали располагаться в области частот составляющие косинусоиды s(t) (теперь это сигнал s₁(t)), показано на рис. 9.

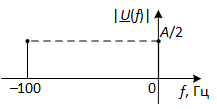
Рис. 9. Вид смещённой на -50 Гц косинусоиды в области частот

Далее усредним полученный сигнал s₁(t) на периоде 0,02 с. В результате усреднения входящая в состав s₁(t) экспонента с частотой -100 Гц () обнуляется, т.к. интервал времени 0,02 с равен двум её собственным периодам. В то же время вторая экспонента с частотой 0 Гц, входящая в состав s₁(t), не обнуляется, результат её усреднения равен A/2. Итак, усреднив сигнал s₁(t) на интервале времени 0,02 с, получим

.

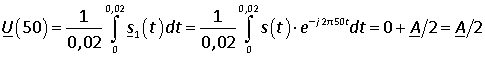Получили то, что хотели, а именно |U(50)|=A/2.

Собственно, в рассмотренных двух процедурах и заключается преобразование Фурье:

1)    смещение частот всех комплексных экспонент, входящих в состав входного сигнала u(t), на значение —f_x для того, чтобы комплексная экспонента с частотой f_x превратилась в постоянную составляющую, тем самым приобретя, так сказать, иммунитет к обнулению через усреднение.

2)    усреднение сигнала со смещёнными частотами на интервале времени, кратном периодам всех комплексных экспонент, входящих в состав сигнала u(t), с целью их обнуления (всех экспонент, кроме той, что превратилась в постоянную составляющую).

В общем случае в состав входного сигнала u(t) входит неограниченное число комплексных экспонент со всевозможными частотами. В этом общем случае процедура 2) работает только на интервале усреднения от -∞ до +∞, поскольку только такой интервал времени кратен любому периоду любой комплексной экспоненты. Итак, получили формулу для преобразования Фурье:

.

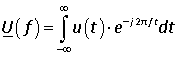Приведённое объяснение преобразования Фурье помогает образному восприятию его сути. Более глубокое понимание этого преобразования и его модификаций (дискретное преобразование Фурье, оконное преобразование Фурье, ряд Фурье, вейвлет-преобразование и т.д.) достигается через понятие свертки функций.