Рассмотрим влияние оконного преобразования Фурье на работу дистанционной защиты. Эта задача возникла в результате обсуждения на форуме бывалого релейщика.
Замер дистанционной защиты – комплексное сопротивление. Комплексное сопротивление рассчитывается из комплексов напряжений и токов, которые, как правило, выделяются с помощью так называемого двухполупериодного (периодного) фильтра Фурье. Этот фильтр Фурье – не что иное, как преобразование Фурье с окном наблюдения в период номинальной частоты сети (20 мс). При этом окно прямоугольное.
Также рассмотрим такой же фильтр Фурье, но с окном. Пусть это будет окно Хемминга (рис. 1).
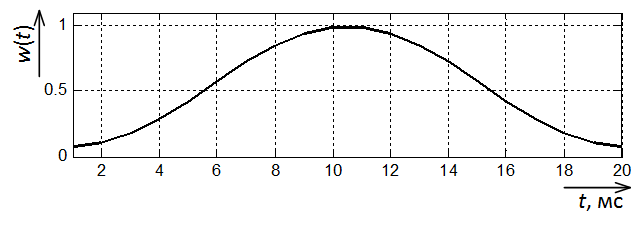Рис. 1. Окно Хемминга
Дистанционная защита реагирует на короткие замыкания, поэтому проверять работу указанных двух фильтров будем на процессе короткого замыкания. При этом ограничимся только током (наверное, пока этого будет достаточно, если понадобится, привлечём ещё и напряжение).
Сначала возьмём сигнал тока без апериодической составляющей переходного процесса (рис. 2).
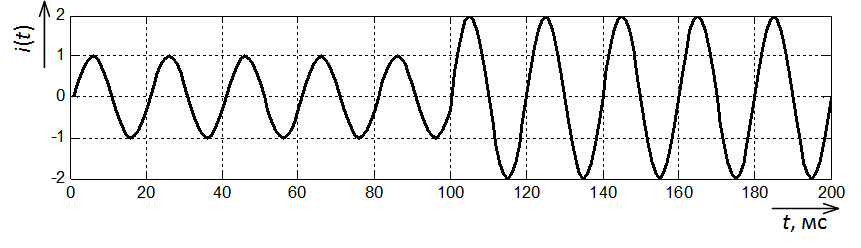
Рис. 2. Осциллограмма тока КЗ без апериодической составляющей
Результаты работы простого фильтра Фурье, без окна, показаны на рис. 3.
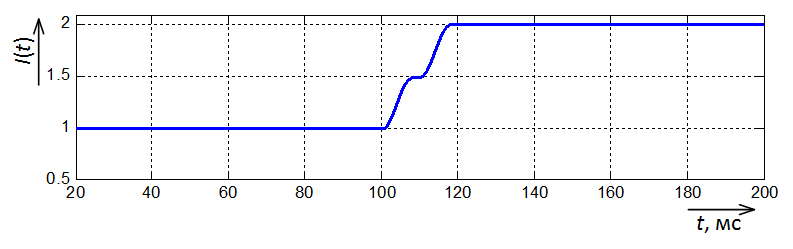Рис. 3. Осциллограмма амплитуды тока на выходе простого фильтра Фурье
Результаты работы фильтра Фурье с окном Хемминга показаны на рис. 4.
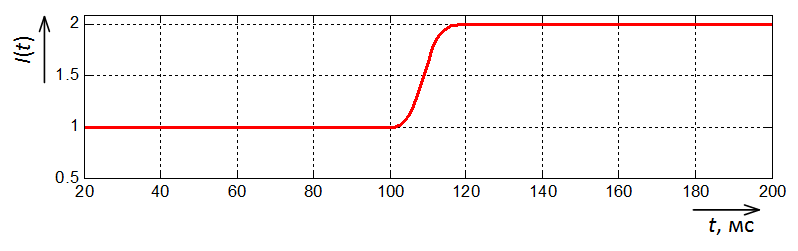
Рис. 4. Осциллограмма амплитуды тока на выходе фильтра Фурье с окном Хемминга
Что мы получили? Не считая переходного процесса в фильтрах, результаты полностью идентичны.
Далее возьмём сигнал тока, содержащий апериодическую составляющую переходного процесса (рис. 5).
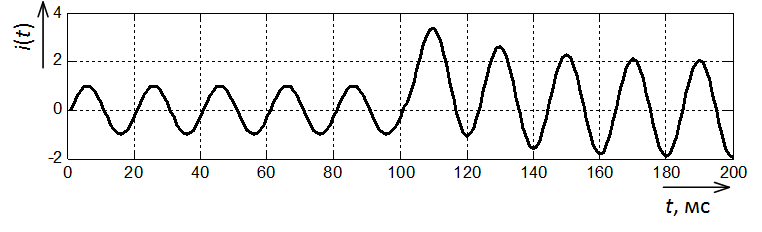
Рис. 5. Осциллограмма тока КЗ с апериодической составляющей
На рис. 6 вместе показаны результаты работы простого фильтра Фурье (синим) и фильтра Фурье с окном Хемминга (красным).
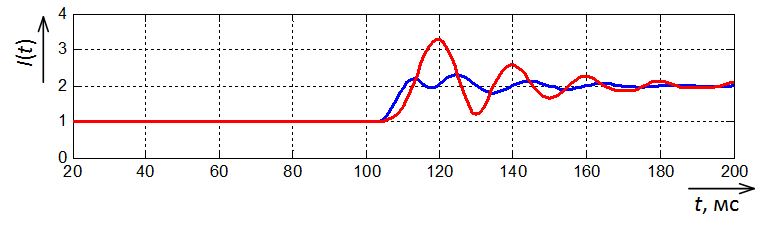
Рис. 6. Осциллограмма амплитуды тока на выходе простого фильтра Фурье и фильтра Фурье с окном Хемминга
Видно, что у Фурье с окном Хемминга довольно приличные колебания, намного больше, чем у простого Фурье. Почему так? Давайте разбираться.
Посмотрим на амплитудно-частотные характеристики обоих фильтров (рис. 7).
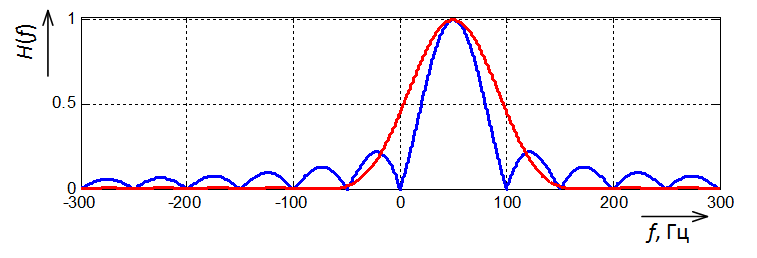
Рис. 7. Амплитудно-частотные характеристики (АЧХ) простого фильтра Фурье (синяя) и фильтра Фурье с окном Хемминга (красная)
Во-первых, замечаем, что фильтр Фурье с окном по сравнению с простым Фурье даёт гораздо меньшие боковые лепестки. Это его плюс. Но какое отношение это имеет к обнаруженным нам колебаниям, идущим от апериодической составляющей? Очевидно, что никакого.
Во-вторых, видим, что основной лепесток АЧХ у оконного Фурье шире, чем у простого Фурье. Это означает, что у него хуже разрешение по частоте. Иными словами, фильтр Фурье с окном хуже различает близкие частоты, они как бы смешиваются друг с другом. В нашем случае важны две достаточно близкие частоты. Это 50 Гц и 0 Гц. В простом фильтре Фурье 0 Гц вообще не подмешивается в 50 Гц, т.е. подавляется на 100 %. Чего нельзя сказать о Фурье с окном. Им составляющая 0 Гц подавляется только на 50 %. Теперь вспомним, что апериодика – это составляющая с частотой 0 Гц… Вот и нашлась причина больших колебаний выхода фильтра с оконным Фурье.
Итак, оконное преобразование Фурье не очень-то подходит для реализации обычных измерительных органов релейной защиты, в частности, реле сопротивления. Лучше использовать обычный фильтр Фурье (ну или что-то совсем другое).