Метод фазных координат: моделирование воздушной линии с ответвительными подстанциями

В процессе исследований может возникнуть задача моделирования воздушной линии (ВЛ) электропередачи с ответвительными подстанциями (рис. 1).

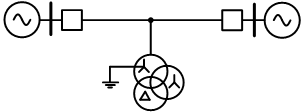
Рис. 1. Воздушная линия с ответвительными подстанциями с трехобмоточным трасформатором со схемой соединения обмоток Y0/Y/Δ

Если не требуется рассматривать режимы КЗ непосредственно в самом трансформаторе подстанции, а требуется учесть токораспределение, вносимое трансформатором с заземлённой нейтралью, то есть два варианта моделирования такой сети. Первый предполагает использовать полную модель трансформатора, однако ввиду сложности подобной модели и значительного числа вычислительных операций расчет модели ВЛ будет происходить крайне медленно. Второй вариант предполагает учитывать факт заземления нейтрали трансформатора простейшим многополюсником.

Согласно [1], сопротивление нулевой последовательности трансформатора возможно принять Z_Т0 = (0,85-0,9)Z_Т. Оттуда же сопротивление трансформатора со стороны высшего напряжения (ВН) по нулевой последовательности вводится сопротивлением обмоток ВН и низшего напряжения (НН) (рис. 2).

Рис. 2. Схема замещения двухобмоточного трансформатора по нулевой последовательности

Аналогично для трёхобмоточного трансформатора, в котором токам нулевой последовательности сопротивляются только обмотки высшего и низшего напряжения, сопротивление нулевой последовательности будет включать в себя сопротивление обмоток сторон ВН и НН (рис. 3).

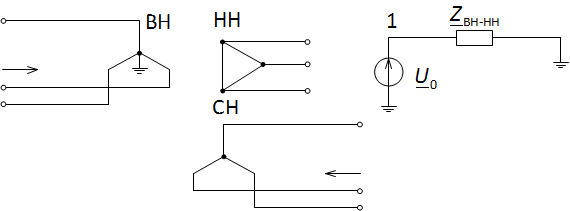
Рис. 3. Схема замещения трёхобмоточного трансформатора (схема соединения обмоток Y0/Y/Δ) по нулевой последовательности

Иными словами, схема замещения трансформатора по прямой последовательности будет иметь вид, представленный на рис. 4.

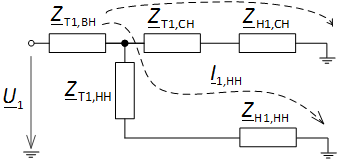
Рис. 4. Схема замещения трехобмоточного трансформатора со схемой соединения обмоток Y0/Y/Δ по прямой последовательности и путь протекания тока прямой последовательности

Схема замещения трансформатора по нулевой последовательности показана на рис. 5.

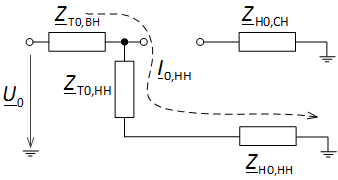
Рис. 5. Схема замещения трёхобмоточного трансформатора со схемой соединения обмоток Y0/Y/Δ по нулевой последовательности и путь протекания тока нулевой последовательности

На рис. 4-5 указаны следующие параметры:

• Z_Т1,ВН, Z_Т0,ВН – сопротивление обмотки ВН по прямой и нулевой последовательности; Z_Т1,СН – сопротивление обмотки СН по прямой последовательности;
• Z_Т1,НН, Z_Т0,НН – сопротивление обмотки НН по прямой и нулевой последовательности;
• Z_Н1,СН, Z_Н1,НН – сопротивление нагрузки по прямой последовательности, подключаемое к обмоткам СН и НН соответственно;
• Z_Н0,СН, Z_Н0,НН – сопротивление нагрузки по нулевой последовательности, подключаемое к обмоткам СН и НН соответственно.

Если вся остальная модель сети построена на основе многополюсников, то схему замещения ответвительного трансформатора также потребуется представить многополюсниками. Она будет иметь вид, представленный на рис. 6. В схему замещения вводится дополнительный многополюсник, сопротивление которого по нулевой последовательности равно нулю, а по прямой последовательности является бесконечно большим. Использование подобного элемента позволяет рассматривать схему замещения трансформатора для прямой и нулевой последовательности (рис. 6) отдельными схемами (рис. 7, 8). Каждый из многополюсников описывается своей матрицей формы A так же, как и модель эквивалентной энергосистемы.

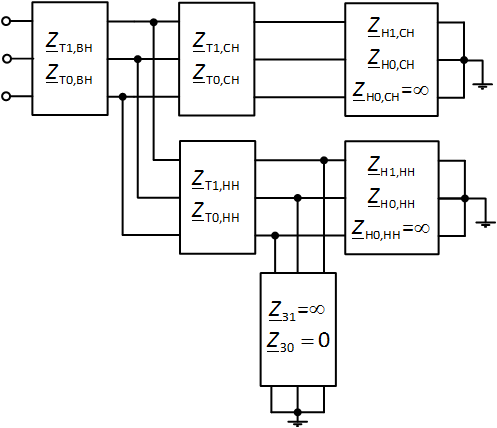
Рис. 6. Схема замещения трёхобмоточного трансформатора в виде многополюсников

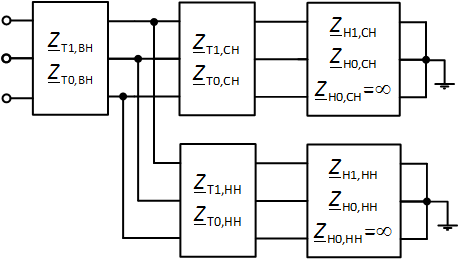
Рис. 7. Схема в виде многополюсников для прямой последовательности

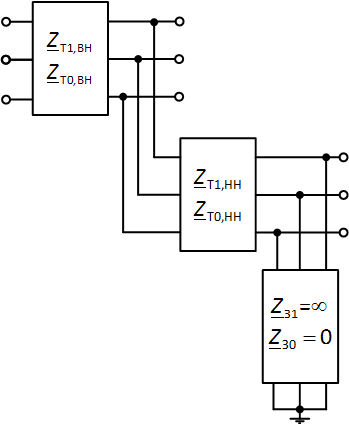
Рис. 8. Схема в виде многополюсников для нулевой последовательности

Таким образом, возможно построение простейшей модели силового трансформатора ответвительной подстанции, расчёт которой требует минимума вычислительных ресурсов.

Список использованной литературы

1. Руководящие указания по релейной защите. Вып. 11. Расчеты токов короткого замыкания для релейной защиты и системной автоматики в сетях 110-750 кВ. – М.: Энергия, 1979, с. 34