Моделирование дифференциального реле с торможением

Дифференциальное реле используется при реализации основных защит различного оборудования: генераторов, трансформаторов, линий электропередачи и др. Применение реле с тормозной характеристикой препятствует неселективному действию защиты.

Пройдите наш онлайн-курс по MATLAB/SIMULINK. Там вы научитесь пользоваться MATLAB как мощным калькулятором, создавать свои модели в SIMULINK, моделировать электрические цепи, а также сложные электроэнергетические системы с устройствами релейной защиты.

На вход дифференциального реле с торможением подаются два замера: дифференциальный и тормозной токи. Вариантов реализации замера тормозного тока много, и они зависят от производителя устройства релейной защиты. Примеры формирования тормозного тока приведены в [1].

Рассмотрим тормозную характеристику дифференциального реле, представленную на рис. 1 [1].

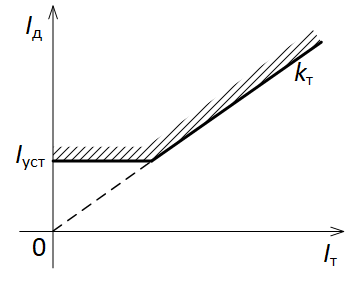
Рис. 1. Тормозная характеристика дифференциального реле

Представленная на рис. 1 тормозная характеристика описывается двумя уравнениями прямых, одна из которых параллельна оси абсцисс, а другая проходит через начало координат. Отсюда следует, что их задания необходимо всего две уставки: уставка дифференциального тока $ I_{\textrm{уст}} $ и коэффициент торможения $ k_{\textrm{т}} $. Срабатывание дифференциального реле с торможением происходит при одновременном выполнении следующих условий:

$$ \begin{cases} I_{\textrm{д}} \ge I_{\textrm{уст}} \\ I_{\textrm{д}} \ge k_{\textrm{т}} I_{\textrm{т}} \end{cases}. $$

Следует учесть, что данное реле, как и обычные реле максимального и минимального действия, обладает коэффициентом возврата $ k_{\textrm{в}} $, поэтому для дифференциального реле необходимо и его задание. Таким образом, выражения, описывающие действие дифференциального реле с торможением, выглядят следующим образом:

$$ y[k] = \begin{cases} 1, \space \textrm{если} \space (I_{\textrm{д}} \ge I_{\textrm{уст}}) \space \textrm{И} \space (I_{\textrm{д}} \ge k_{\textrm{т}} I_{\textrm{т}}) \\ y[k-1], \space \textrm{если} \space (k_{\textrm{в}} I_{\textrm{уст}} \le I_{\textrm{д}} \lt I_{\textrm{уст}}) \space \textrm{И} \space (k_{\textrm{в}} k_{\textrm{т}} I_{\textrm{т}} \le I_{\textrm{д}} \lt k_{\textrm{т}} I_{\textrm{т}}) \\ \textrm{иначе} \space 0 \end{cases} $$

где $ y[k] $ – выходное значение реле в дискретный момент времени $ k $, $ y[k-1] $ – выходное значение реле в предшествующий момент времени.

Вариант реализации представленного дифференциального реле с торможением в Simulink вы можете приобрести в магазине. Вид схемы приведён на рис. 2.

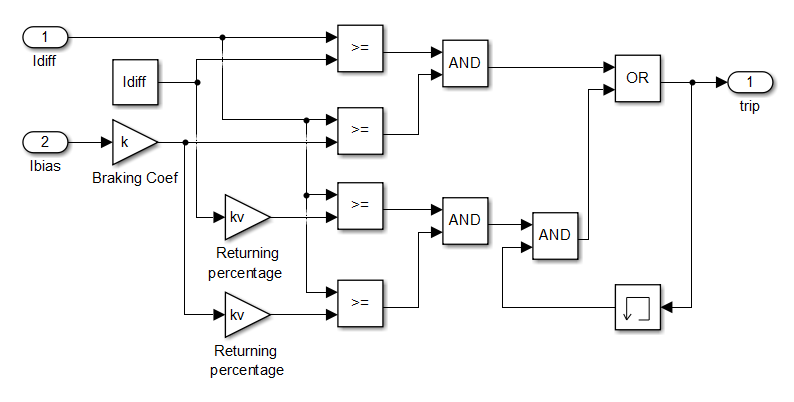
Рис. 2. Реализация дифференциального реле с торможением в Simulink

Протестируем полученное реле. Для этого будем использовать схему, представленную на рис. 3.

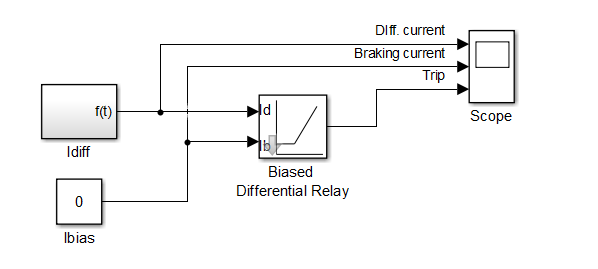
Рис. 3. Схема для тестирования дифференциального реле с торможением в Simulink

Выставим уставки реле $ I_{\textrm{уст}} = 1 $, $ k_{\textrm{т}} = 0.5 $, $ k_{\textrm{в}} = 0.85 $. На вход будем подавать изменяемый дифференциальный ток при постоянном тормозном токе. Проверим правильность срабатывания реле и его коэффициент возврата.

Для начала подадим нулевой тормозной ток. На рис. 4 приведены результаты срабатывания реле. Видим срабатывание реле при $ I_{\textrm{д}} = 1 $ и возврат реле при $ I_{\textrm{д}} = 0.85 $. Коэффициент возврата обеспечивается.

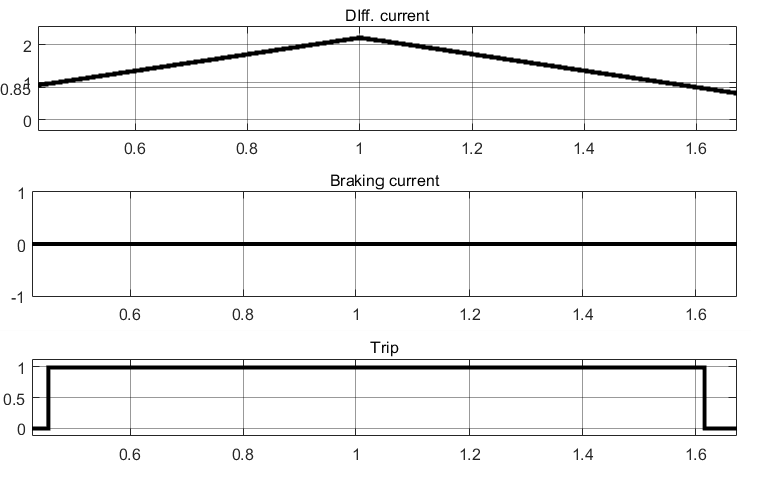
Рис. 4. Результаты тестирования дифференциального реле при нулевом тормозном токе

Подадим тормозной ток, равный 4 А. На рис. 5 приведены результаты срабатывания реле. Видим срабатывание реле при $ I_{\textrm{д}} = 2 $ и возврат реле при $ I_{\textrm{д}} = 1.7 $. Проверим правильность срабатывания реле. Рассчитаем ожидаемое значение дифференциального тока, необходимого для срабатывания реле при указанном значении тормозного тока:

$$ I_{\textrm{д,сраб}} = k_{\textrm{т}} \cdot I_{\textrm{т}} = 0.5 \cdot 4 = 2 \space \textrm{А} $$

Таким образом, реле срабатывает правильно. Коэффициент возврата также обеспечивается.

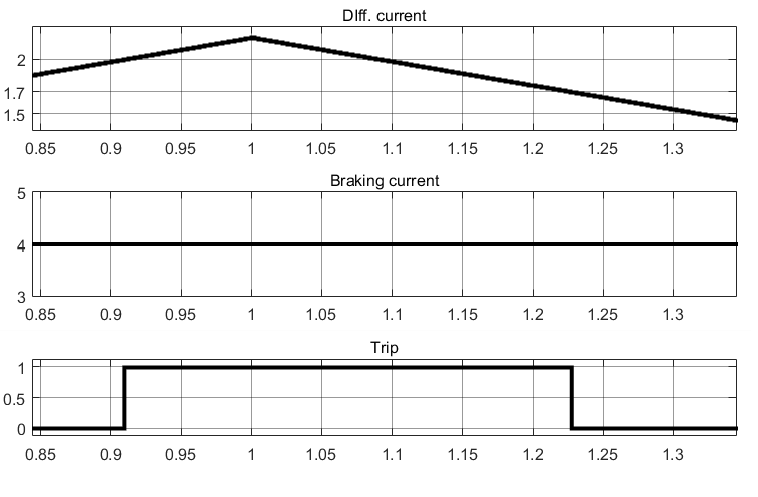
Рис. 5. Результаты тестирования дифференциального реле при ненулевом тормозном токе

Итак, мы смоделировали и протестировали дифференциальное реле с торможением.

Список использованной литературы

1. Шнеерсон Э.М. Цифровая релейная защита. ­­– М.: Энергоатомиздат, 2007.