В программу онлайн-расчёта электрических цепей добавлен функционал расчёта по методу эквивалентного генератора.
Для расчёта тока в ветви по методу эквивалентного генератора необходимо выбрать метод расчёта «МЭГ». После этого необходимо определить все ветви рассчитываемой цепи с помощью кнопки «Ветви» и выбрать ветвь, в которой необходимо рассчитать ток, в полученном спадающем списке. Суть метода эквивалентного генератора приведена здесь.
Для расчёта тока в ветви по методу эквивалентного генератора программа рассчитывает напряжение холостого хода $ \underline{U}_\textrm{хх} $ на выводах разомкнутой ветви с искомым током и внутреннее сопротивление цепи $ \underline{Z}_\textrm{вн} $ относительно ветви с искомым током.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1
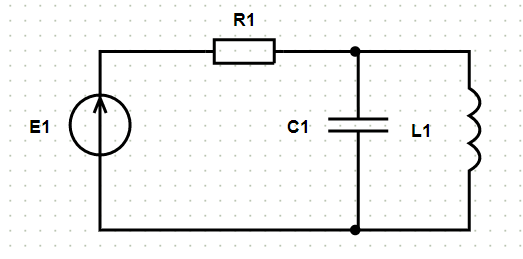
После выбора ветви «L1» и нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:
Рассчитаем ток $ \underline{I} $ в ветви с элементами $ L_{1} $ по методу эквивалентного генератора. Для этого рассчитаем напряжение холостого хода на выводах разомкнутой ветви с искомым током и эквивалентное сопротивление пассивной цепи относительно ветви с искомым током.

Рассчитаем напряжение холостого хода. На рисунке ниже приведена рассчитываемая схема. Напряжение холостого хода $ \underline{U}_\textrm{хх} $ сонаправлено с искомым током. Принятое направление искомого тока приведено на схеме выше.
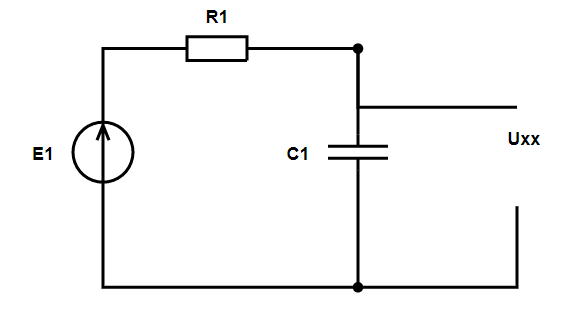
В исходной схеме только один контур. Рассчитаем её по закону Ома.
Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ \underline{I} $ направление источника ЭДС $ \underline{E}_{1} $:
$$ (R_{1}-jX_{C1})\cdot \underline{I} = \underline{E}_{1} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ (1-1j)\cdot \underline{I}=100 $$
Отсюда искомый ток в цепи равен
$$ \underline{I} = 50+50j\space \textrm{А} $$
Определим искомое напряжение холостого хода. Рассмотрим контур, проходящий в указанном порядке через элементы $ \underline{U}_\textrm{хх} $, $ R_{1} $, $ \underline{E}_{1} $, и составим для него уравнение по второму закону Кирхгофа. Получим:
$$ \underline{U}_\textrm{хх}-\underline{I}_{1} \cdot R_{1}=-\underline{E}_{1} $$
Определим напряжение холостого хода. Получим:
$$ \underline{U}_\textrm{хх} = \underline{I}_{1} \cdot R_{1}-\underline{E}_{1}=(50+50j) \cdot 1-100=-50+50j\space\textrm{В} $$
Рассчитаем внутреннее сопротивление цепи $ \underline{Z}_\textrm{вн} $ относительно ветви с искомым током. Для этого из исходной схемы уберём ветвь с искомым током, при этом оставим концы этой ветви. Все источники ЭДС закоротим, а источники тока разомкнем.
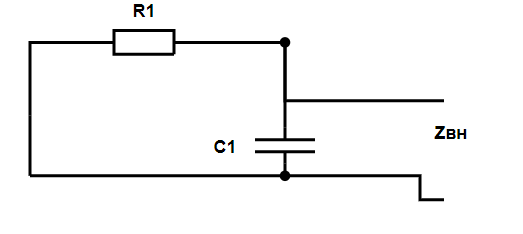
Рассчитаем эквивалентное сопротивление цепи относительно ветви с искомым током.
Ветвь с элементами $ R_{1} $ параллельна ветви с элементами $ C_{1} $. Эквивалентное сопротивление этих ветвей равно:
$$ \underline{Z}_{1} = \frac{R_{1}⋅(- jX_{C1})}{R_{1}- jX_{C1}}=\frac{1⋅(-1j)}{1-1j}=0.5000-0.5000j $$
Внутреннее сопротивление цепи равно:
$$ \underline{Z}_\textrm{вн} = \underline{Z}_{1}+0=0.5000-0.5000j+0=0.5000-0.5000j\space\textrm{Ом} $$
Определим искомый ток:
$$ \underline{I} = \frac{\underline{U}_\textrm{хх}}{\underline{Z}_\textrm{вн}+jX_{L1}} = \frac{-50+50j}{0.5000-0.5000j+1j} =100j\space\textrm{А} $$