Расчёт электрических цепей онлайн по методу контурных токов

В программе онлайн-расчёта электрических цепей появился расчёт по методу контурных токов.

Выбор метода расчёта осуществляется в спадающем списке. Для расчёта по методу контурных токов необходимо выбрать метод расчёта «МКТ». Используемая методика при расчёте по методу узловых потенциалов приведена здесь.

Пример схемы и расчёт:

Исходные данные и схема:

• E1:
  • Номер элемента: 1
  • Амплитудное значение: 100 В
  • Начальная фаза, °: 0
• R1:
  • Номер элемента: 1
  • Сопротивление, Ом: 1
• L1:
  • Номер элемента: 1
  • Сопротивление, Ом: 1
• C1:
  • Номер элемента: 1
  • Сопротивление, Ом: 1

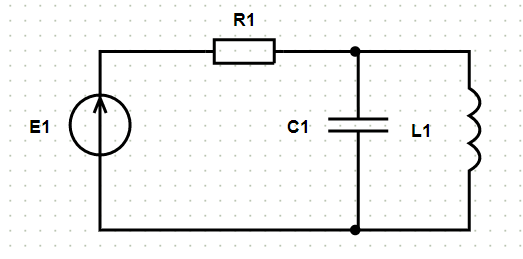
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:

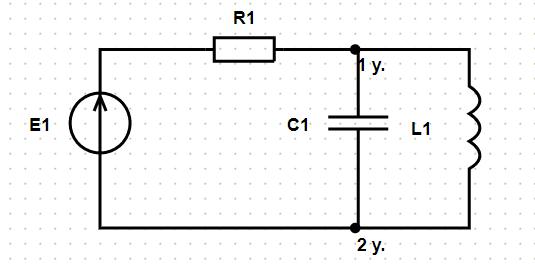
Рассчитаем схему по методу контурных токов.

В данной схеме: узлов − 2, ветвей − 3, независимых контуров − 2.

Количество уравнений, составляемых по методу контурных токов, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей без источников тока, $ N_\textrm{у} $ − число узлов.

Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 3 − 2 + 1 = 2.

Произвольно зададим направления обхода контуров и соответствующие контурные токи.

Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{11} $.
Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{22} $.

Составим уравнения по методу контурных токов.

Составим уравнение для контура №1:

$$ \underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1}=\underline{E}_{1} $$

Составим уравнение для контура №2:

$$ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1}=0 $$

Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:

$$ \begin{cases}\underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1} = \underline{E}_{1} \\ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1} = 0 \\ \end{cases} $$

Подставим в полученную систему уравнений значения сопротивлений и источников и получим:

$$ \begin{cases}(1+1j)\cdot \underline{I}_{11}+ j \cdot \underline{I}_{22}=100 \\ j \cdot \underline{I}_{11}=0 \\ \end{cases} $$

Решим систему уравнений и получим искомые контурные токи:

$$ \underline{I}_{11} = 0\space\textrm{А} $$

$$ \underline{I}_{22} = -100j\space\textrm{А} $$

Произвольно зададим направления токов в ветвях.

Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.

Рассчитаем токи в ветвях исходя из полученных контурных токов.

$$ \underline{I}_{1} =\underline{I}_{11}=0=0 $$ $$ \underline{I}_{2} =\underline{I}_{11}+\underline{I}_{22}=0+(-100j)=-100j $$ $$ \underline{I}_{3} =-\underline{I}_{22}=-(-100j)=100j $$

После завершения расчёта на экран также выводятся векторные диаграммы токов и напряжений.