Эквивалентные преобразования в электрических цепях

При расчёте электрических цепей грамотно проведённые преобразования позволяют уменьшить число уравнений, описывающих работу схемы. Далее приведены основные эквивалентные преобразования.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

• Последовательное соединение пассивных элементов
• Параллельное соединение пассивных элементов
• Параллельное соединение большого количества ветвей
• Параллельное соединение ветвей с источниками ЭДС
• Преобразование источника ЭДС в источник тока
• Преобразование источника тока в источник ЭДС
• Преобразование звезды сопротивлений в треугольник
  • Калькулятор преобразования звезды сопротивлений в треугольник
• Преобразование треугольника сопротивлений в звезду
  • Калькулятор преобразования треугольника сопротивлений в звезду

Последовательное соединение пассивных элементов

Пример схемы приведён на рис. 1.

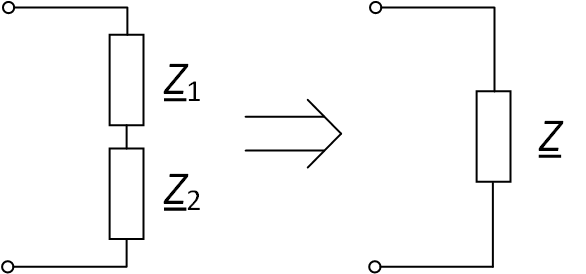
Рис. 1. Преобразование последовательно соединённых элементов

Эквивалентное сопротивление определяется по формуле

$$ \underline{Z}={{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}. $$

В общем случае при последовательном соединении N элементов

$$ \underline{Z}=\sum\limits_{i=1}^{N}{{{\underline{Z}}_{i}}}. $$

Параллельное соединение пассивных элементов

Пример схемы приведён на рис. 2.

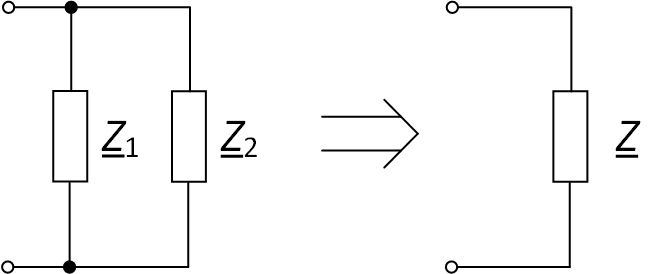
Рис. 2. Преобразование параллельно соединённых элементов

Эквивалентное сопротивление определяется по формуле

$$ \underline{Z}=\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Параллельное соединение большого количества ветвей

Пример схемы приведён на рис. 3.

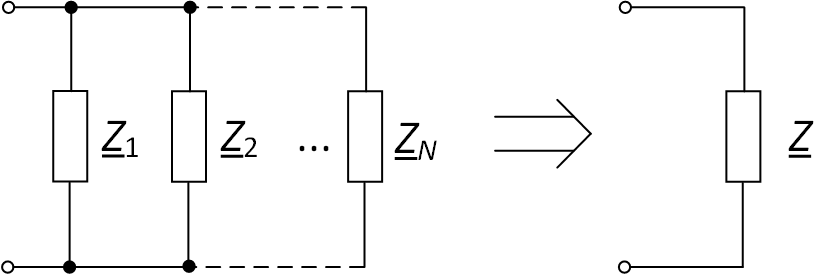
Рис. 3. Преобразование параллельно соединённых ветвей

Эквивалентное сопротивление определяется по формуле

$$ \underline{Z}=\frac{1}{\sum\limits_{i=1}^{N}{\frac{1}{{{\underline{Z}}_{i}}}}}. $$

Параллельное соединение ветвей с источниками ЭДС

Пример схемы приведён на рис. 4.

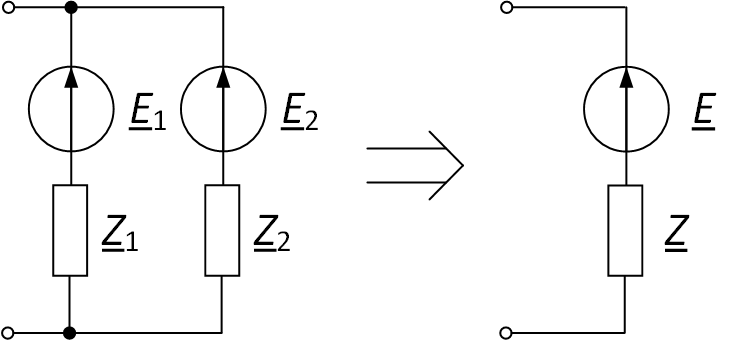
Рис. 4. Преобразование параллельно соединённых ветвей с источниками ЭДС

Эквивалентное сопротивление определяется по формуле

$$ \underline{Z}=\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Эквивалентная ЭДС определяется по формуле

$$ \underline{E}=\frac{{{\underline{E}}_{1}}{{\underline{Z}}_{2}}+{{\underline{E}}_{2}}{{\underline{Z}}_{1}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

В общем случае при параллельном соединении N ветвей с источниками ЭДС эквивалентное сопротивление определяется по формуле

$$ \underline{Z}=\frac{1}{\sum\limits_{i=1}^{N}{\frac{1}{{{\underline{Z}}_{i}}}}}. $$

Эквивалентная ЭДС при параллельном соединении N ветвей определяется по формуле

$$ \underline{E}=\frac{\sum\limits_{i=1}^{N}{\frac{{{\underline{E}}_{i}}}{{{\underline{Z}}_{i}}}}}{\sum\limits_{i=1}^{N}{\frac{1}{{{\underline{Z}}_{i}}}}}. $$

Преобразование источника ЭДС в источник тока

Пример схемы приведён на рис. 5.

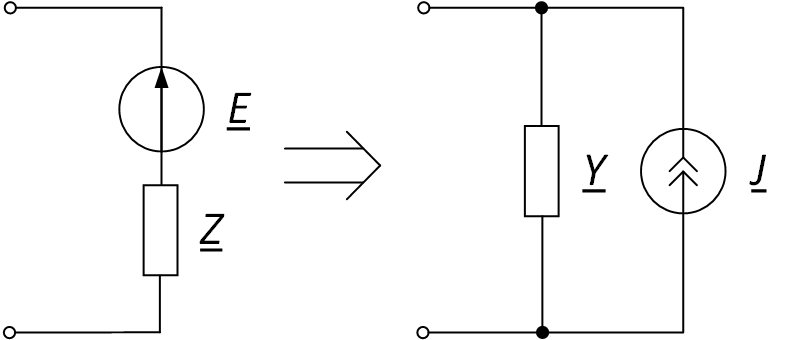
Рис. 5. Преобразование источника ЭДС в источник тока

Сила тока источника тока определяется по формуле

$$ \underline{J}=\frac{\underline{E}}{\underline{Z}}. $$

Проводимость ветви, параллельной источнику току, определяется по формуле

$$ \underline{Y}=\frac{1}{\underline{Z}}. $$

Преобразование источника тока в источник ЭДС

Пример схемы приведён на рис. 6.

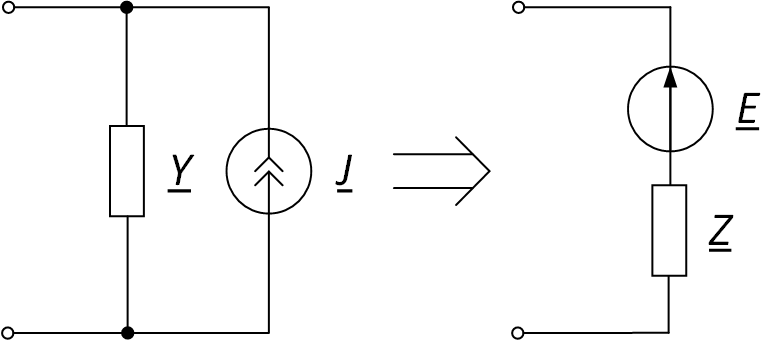
Рис. 6. Преобразование источника тока в источник ЭДС

ЭДС определяется по формуле

$$ \underline{E}=\frac{\underline{J}}{\underline{Y}}. $$

Сопротивление определяется по формуле

$$ \underline{Z}=\frac{1}{\underline{Y}}. $$

Преобразование звезды сопротивлений в треугольник

Пример схемы приведён на рис. 7.

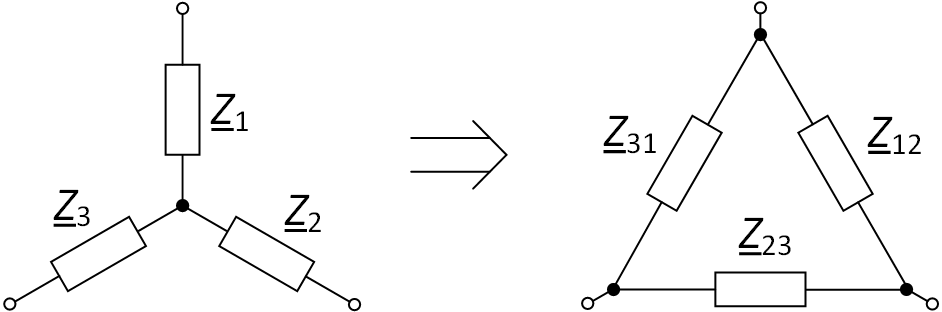
Рис. 7. Преобразование звезды в треугольник

Сопротивления треугольника определяются по формулам

$$ {{\underline{Z}}_{12}}={{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}+\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{3}}}, $$

$$ {{\underline{Z}}_{23}}={{\underline{Z}}_{2}}+{{\underline{Z}}_{3}}+\frac{{{\underline{Z}}_{2}}\cdot {{\underline{Z}}_{3}}}{{{\underline{Z}}_{1}}}, $$

$$ {{\underline{Z}}_{31}}={{\underline{Z}}_{1}}+{{\underline{Z}}_{3}}+\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{3}}}{{{\underline{Z}}_{2}}}. $$

Калькулятор преобразования звезды сопротивлений в треугольник

Преобразование треугольника сопротивлений в звезду

Пример схемы приведён на рис. 8.

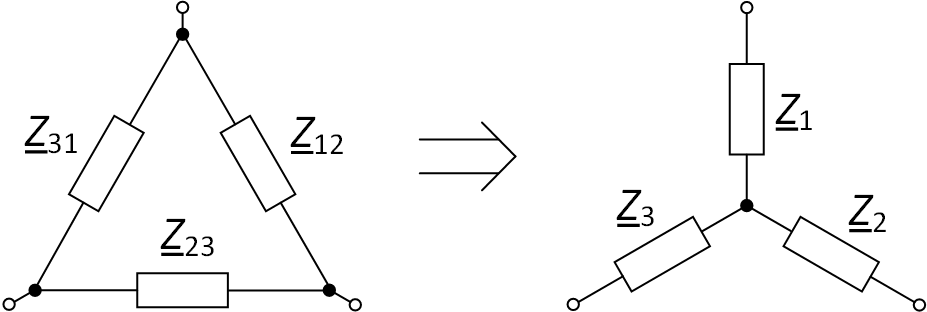
Рис. 8. Преобразование треугольника в звезду

Сопротивления звезды определяются по формулам

$$ {{\underline{Z}}_{1}}=\frac{{{\underline{Z}}_{31}}\cdot {{\underline{Z}}_{12}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}, $$

$$ {{\underline{Z}}_{2}}=\frac{{{\underline{Z}}_{23}}\cdot {{\underline{Z}}_{12}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}, $$

$$ {{\underline{Z}}_{3}}=\frac{{{\underline{Z}}_{31}}\cdot {{\underline{Z}}_{23}}}{{{\underline{Z}}_{12}}+{{\underline{Z}}_{31}}+{{\underline{Z}}_{23}}}. $$

Калькулятор преобразования треугольника сопротивлений в звезду

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.