В дополнение к выводу метода рассмотрим методику расчёта электрических цепей по методу узловых потенциалов.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
Последовательность расчёта следующая.
- Пронумеровать все узлы и задать произвольное направление токов в схеме.
- Стянуть узлы с одинаковым потенциалом. Узлы будут иметь одинаковый потенциал, если между ними находится чистая ветвь с нулевым сопротивлением – закоротка (ветви между узлами 2 − 4 и 3 − 5 на рис. 1). Перерисовывать схему со стянутыми узлами не обязательно, но тогда следует учесть, что потенциалы узлов по концам закоротки будут одинаковыми.
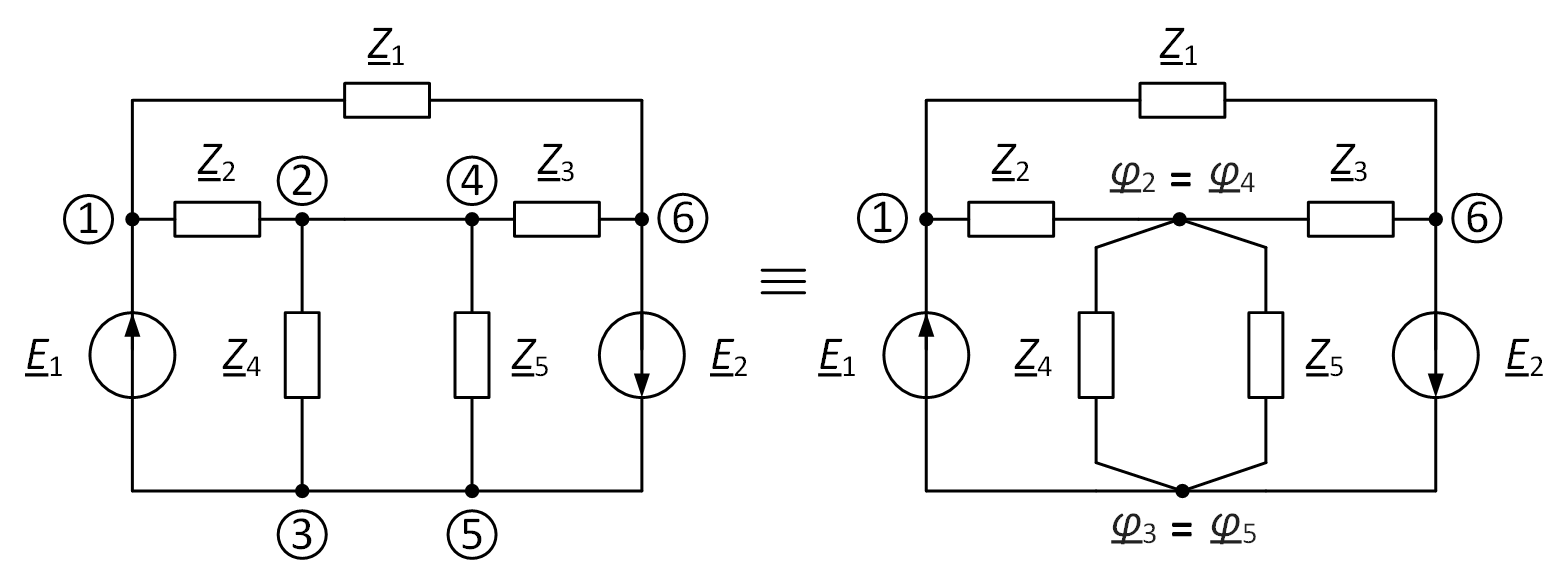
Рис. 1. Пример объединения узлов с одинаковым потенциалом
- Выбрать базисный узел (рис. 2) и приравнять его потенциал нулю $ \underline{\varphi}_{3} = 0 \space \textrm{В} $. В качестве базисного узла можно выбрать любой, за исключением случая, когда имеются особые ветви. Если в схеме есть хотя бы одна особая ветвь, то за базисный узел следует принимать один из концов одной из таких ветвей. При этом потенциал другого конца будет равен ЭДС $ \underline{\varphi}_{1} = \underline{E}_{1} $, если источник напряжения направлен в этот узел, и равен минус ЭДС $ \underline{\varphi}_{6} =- \underline{E}_{2} $, если источник направлен к базисному узлу.
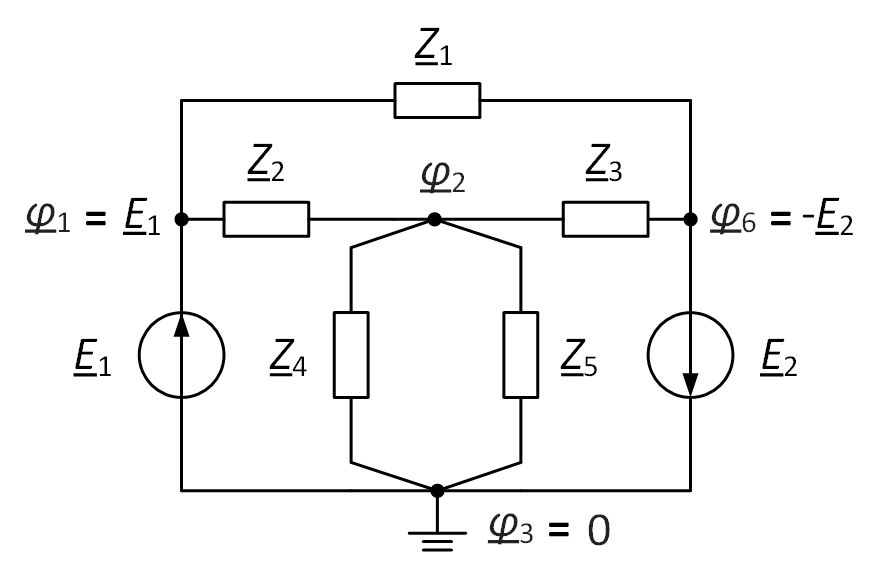
Рис. 2. Выбор базисного узла
Примечание. Зачастую для обозначения базисного узла используют символ заземления, так как принято считать, что «земля» имеет нулевой потенциал.

- Составить уравнения для узлов без особых ветвей, потенциалы которых неизвестны. Уравнения записываются по следующему принципу:
- потенциал рассматриваемого узла умножается на сумму проводимостей всех примыкающих к нему ветвей;
- вычитаются потенциалы узлов, находящихся на противоположных концах примыкающих ветвей, умноженные каждый на свою проводимость соединяющей их ветви;
- приравнивается алгебраической сумме примыкающих к данному узлу источников тока и источников ЭДС, последние умножаются на проводимость ветви, в которой они расположены.
Под алгебраической суммой подразумевается необходимость учёта направленности источников, если источник направлен в рассматриваемый узел, то он записывается со знаком «+», в противном случае со знаком «-».
В случае, если имеется более одной особой ветви, и они не имеют общие узлы, то уравнения для узлов, в состав которых входит особая ветвь, не примыкающая к базисному узлу, записываются следующим образом:
- потенциал рассматриваемого узла умножается на сумму проводимостей всех примыкающих к нему ветвей и проводимостей ветвей, примыкающих к узлу противоположного конца особой ветви;
- вычитаются потенциалы узлов, находящихся на противоположных концах примыкающих ветвей к узлам особой ветви, умноженные каждый на свою проводимость примыкающей ветви;
- приравнивается алгебраической сумме примыкающих к узлам особой ветви источников тока и источников ЭДС, последние умножаются на проводимость ветви, в которой они расположены, за исключением источника ЭДС особой ветви, который умножается на сумму проводимости ветвей, примыкающих к узлу противоположного конца особой ветви.
- При составлении уравнения проводимость особой ветви не учитывается (1/0=∞). Следует также учитывать, что направление ЭДС особой ветви и соответственно её знак учитываются относительно рассматриваемого узла.
- Рассчитать токи в ветвях по закону Ома как алгебраическую сумму разности потенциалов и ЭДС в ветви с искомым током, делённую на сопротивление этой ветви. Вычитаемым будет тот потенциал, в который направлен ток, а знак ЭДС выбирается в зависимости от направления: в случае сонаправленности с током ЭДС берётся со знаком «+», в противном случае со знаком «-». Ток в закоротке следует искать по первому закону Кирхгофа, составленному для одного из узлов рассматриваемой ветви в исходной схеме, после расчета всех остальных токов в схеме.
- Правильность расчёта по методу узловых потенциалов проще всего проверить по первому закону Кирхгофа для уникальных узлов без особых ветвей, подставив полученные значения токов. Под уникальными узлами подразумеваются те узлы, при рассмотрении которых имеется хотя бы одна ветвь, не примыкающая к другим из рассмотренных узлов.
Пример решения. В качестве примера рассмотрим схему с двумя особыми ветвями и источником тока (рис. 3). Количество уравнений составляемых для нахождения узловых потенциалов равно
6 (всего узлов) – 1 (базисный узел) – 2 (узла особых ветвей) = 3.
Произвольно обозначим узлы и токи на схеме. Один из узлов одной из особой ветви (1-4 и 3-6) примем за базисный, к примеру узел 4, в таком случае $ \underline{\varphi}_{4} = 0 $, а $ \underline{\varphi}_{1} = \underline{E}_{1} $.
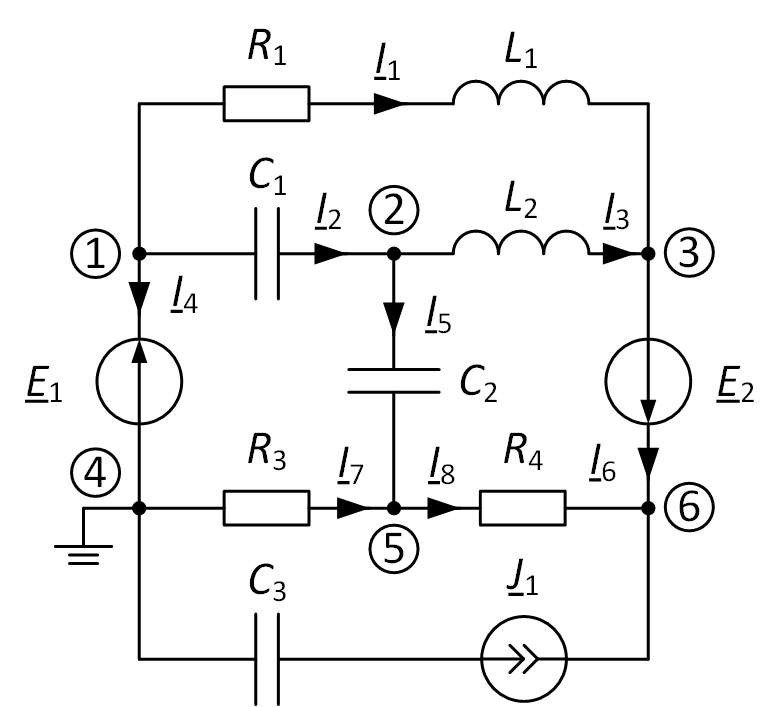
Рис. 3. Пример расчёта электрической схемы
В ветви 3-6 необходимо найти потенциал только одного из узлов (рассчитаем для узла 6), так как второй (потенциал узла 3) будет отличаться на значение ЭДС, т.е. $ \underline{\varphi}_{3} = \underline{\varphi}_{6}- \underline{E}_{2} $. Далее необходимо составить уравнения для нахождения оставшихся потенциалов в узлах 2, 5 и 6. Следует отметить, что ёмкость ветви с источником тока не повлияет на расчёты, поскольку проводимость этой ветви бесконечно большая, а ток задаётся самим источником.
$$ \begin{cases} \underline{\varphi}_{5} \cdot (\underline{Y}_{7} + \underline{Y}_{5} + \underline{Y}_{8})- \underline{\varphi}_{4} \cdot \underline{Y}_{7}- \underline{\varphi}_{2} \cdot \underline{Y}_{5}- \underline{\varphi}_{6} \cdot \underline{Y}_{8} = 0 \\ \underline{\varphi}_{2} \cdot (\underline{Y}_{2} + \underline{Y}_{5} + \underline{Y}_{3})- \underline{\varphi}_{1} \cdot \underline{Y}_{2}- \underline{\varphi}_{5} \cdot \underline{Y}_{5}- \underline{\varphi}_{3} \cdot \underline{Y}_{3} = 0 \\ \underline{\varphi}_{6} \cdot (\underline{Y}_{8} + \underline{Y}_{3} + \underline{Y}_{1})- \underline{\varphi}_{5} \cdot \underline{Y}_{8}- \underline{\varphi}_{2} \cdot \underline{Y}_{3}- \underline{\varphi}_{1} \cdot \underline{Y}_{1} = \underline{E}_{2} \cdot (\underline{Y}_{3} + \underline{Y}_{1}) + \underline{J}_{1} \end{cases} $$
где
$$ {{\underline{Y}}_{1}}=\frac{1}{{{\underline{Z}}_{1}}}=\frac{1}{{{R}_{1}}+j\omega \cdot {{L}_{1}}}; $$
$$ {{\underline{Y}}_{2}}=\frac{1}{{{\underline{Z}}_{2}}}=-j\omega \cdot {{C}_{1}}; $$
$$ {{\underline{Y}}_{3}}=\frac{1}{{{\underline{Z}}_{3}}}=j\frac{1}{\omega \cdot {{L}_{2}}}; $$
$$ {{\underline{Y}}_{5}}=\frac{1}{{{\underline{Z}}_{5}}}=-j\omega \cdot {{C}_{2}}; $$
$$ {{\underline{Y}}_{7}}=\frac{1}{{{\underline{Z}}_{7}}}=\frac{1}{{{R}_{3}}}; $$
$$ {{\underline{Y}}_{8}}=\frac{1}{{{\underline{Z}}_{8}}}=\frac{1}{{{R}_{4}}}. $$
Подставим известные значения потенциалов, сократив количество неизвестных:
$$ \begin{cases} \underline{\varphi}_{5} \cdot (\underline{Y}_{7} + \underline{Y}_{5} + \underline{Y}_{8})- 0 \cdot \underline{Y}_{7}- \underline{\varphi}_{2} \cdot \underline{Y}_{5}- \underline{\varphi}_{6} \cdot \underline{Y}_{8} = 0 \\ \underline{\varphi}_{2} \cdot (\underline{Y}_{2} + \underline{Y}_{5} + \underline{Y}_{3})- \underline{E}_{1} \cdot \underline{Y}_{2}- \underline{\varphi}_{5} \cdot \underline{Y}_{5}- (\underline{\varphi}_{6}- \underline{E}_{2}) \cdot \underline{Y}_{3} = 0 \\ \underline{\varphi}_{6} \cdot (\underline{Y}_{8} + \underline{Y}_{3} + \underline{Y}_{1})- \underline{\varphi}_{5} \cdot \underline{Y}_{8}- \underline{\varphi}_{2} \cdot \underline{Y}_{3}- \underline{E}_{1} \cdot \underline{Y}_{1} = \underline{E}_{2} \cdot (\underline{Y}_{3} + \underline{Y}_{1}) + \underline{J}_{1} \end{cases} $$
Перенесём все свободные составляющие в правую часть равенств и получим конечную систему уравнений с тремя неизвестными узловыми потенциалами:
$$ \begin{cases} \underline{\varphi}_{5} \cdot (\underline{Y}_{7} + \underline{Y}_{5} + \underline{Y}_{8})- \underline{\varphi}_{2} \cdot \underline{Y}_{5}- \underline{\varphi}_{6} \cdot \underline{Y}_{8} = 0 \\ \underline{\varphi}_{2} \cdot (\underline{Y}_{2} + \underline{Y}_{5} + \underline{Y}_{3})- \underline{\varphi}_{5} \cdot \underline{Y}_{5}- \underline{\varphi}_{6} \cdot \underline{Y}_{3} = \underline{E}_{1} \cdot \underline{Y}_{2}- \underline{E}_{2} \cdot \underline{Y}_{3} \\ \underline{\varphi}_{6} \cdot (\underline{Y}_{8} + \underline{Y}_{3} + \underline{Y}_{1})- \underline{\varphi}_{5} \cdot \underline{Y}_{8}- \underline{\varphi}_{2} \cdot \underline{Y}_{3} = \underline{E}_{1} \cdot \underline{Y}_{1} + \underline{E}_{2} \cdot (\underline{Y}_{3} + \underline{Y}_{1}) + \underline{J}_{1} \end{cases} $$
Для решения системы уравнений с неизвестными узловыми потенциалами, можно воспользоваться Matlab. Для этого представим систему уравнений в матричной форме:
$$ \begin{bmatrix} \underline{Y}_{7} + \underline{Y}_{5} + \underline{Y}_{8} & -\underline{Y}_{5} & -\underline{Y}_{8} \\ -\underline{Y}_{5} & \underline{Y}_{2} + \underline{Y}_{5} + \underline{Y}_{3} & -\underline{Y}_{3} \\ -\underline{Y}_{8} & -\underline{Y}_{3} & \underline{Y}_{8} + \underline{Y}_{3} + \underline{Y}_{1} \end{bmatrix} \cdot \begin{bmatrix} \underline{\varphi}_{5} \\ \underline{\varphi}_{2} \\ \underline{\varphi}_{6} \end{bmatrix} = \\ = \begin{bmatrix} 0 \\ \underline{E}_{1} \cdot \underline{Y}_{2}- \underline{E}_{2} \cdot \underline{Y}_{3} \\ \underline{E}_{1} \cdot \underline{Y}_{1} + \underline{E}_{2} \cdot (\underline{Y}_{3} + \underline{Y}_{1}) + \underline{J}_{1} \end{bmatrix} $$
Запишем скрипт в Matlab для нахождения неизвестных:
>> syms Y1 Y2 Y3 Y5 Y7 Y8 E1 E2 J1;
>> A = [Y7+Y5+Y8 -Y5 -Y8;
-Y5 Y2+Y5+Y3 -Y3;
-Y8 -Y3 Y8+Y3+Y1];
>> B = [ 0;
E1*Y2-E2*Y3;
E1*Y1+E2*(Y3+Y1)+J1];
>> fi=A\B
Примечание. Для решения в численном виде необходимо заменить символьное задание переменных реальными значениями проводимостей, ЭДС и тока источника.
В результате получим вектор-столбец $ \underline{\boldsymbol{\varphi}} $ из трёх элементов, состоящий из искомых узловых потенциалов, при этом токи в ветвях через потенциалы узлов:
$$ {{\underline{I}}_{1}}=\frac{{{\underline{\varphi }}_{1}}-{{\underline{\varphi }}_{3}}}{{{\underline{Z}}_{1}}}, $$
$$ {{\underline{I}}_{2}}=\frac{{{\underline{\varphi }}_{1}}-{{\underline{\varphi }}_{2}}}{{{\underline{Z}}_{2}}}, $$
$$ {{\underline{I}}_{3}}=\frac{{{\underline{\varphi }}_{2}}-{{\underline{\varphi }}_{3}}}{{{\underline{Z}}_{3}}}, $$
$$ {{\underline{I}}_{5}}=\frac{{{\underline{\varphi }}_{2}}-{{\underline{\varphi }}_{5}}}{{{\underline{Z}}_{5}}}, $$
$$ {{\underline{I}}_{7}}=\frac{{{\underline{\varphi }}_{4}}-{{\underline{\varphi }}_{5}}}{{{\underline{Z}}_{7}}}, $$
$$ {{\underline{I}}_{8}}=\frac{{{\underline{\varphi }}_{5}}-{{\underline{\varphi }}_{6}}}{{{\underline{Z}}_{8}}}, $$
где
$$ \underline{\varphi}_{3} = \underline{\varphi}_{6}- \underline{E}_{2}. $$
Для проверки правильности расчёта можно воспользоваться уравнениями по первому закону Кирхгофа: если суммы токов в узлах 2 и 5 равны нулям, значит расчёт выполнен верно:
$$ \underline{I}_{5} + \underline{I}_{3}- \underline{I}_{2} = 0, $$
$$ \underline{I}_{5} + \underline{I}_{7}- \underline{I}_{8} = 0. $$
Итак, метод узловых потенциалов позволяет рассчитывать меньшее количество сложных уравнений для расчёта электрической цепи в сравнении с другими методами при меньшем числе узлов в сравнении с количеством контуров.