Формула «чужого» сопротивления

Формула «чужого» сопротивления позволяет определить токи в параллельных ветвях при известном токе в ветви, подходящей к данным ветвям.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Рассмотрим схему, представленную на рис. 1.

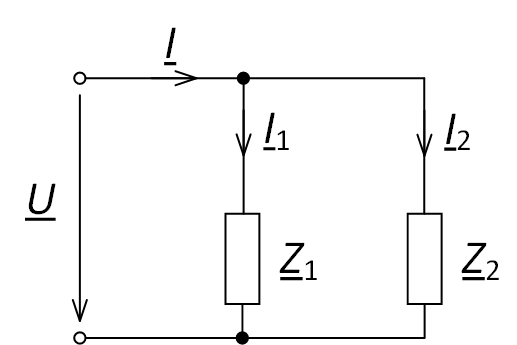
Рис. 1. Схема для определения токов в ветвях по формуле «чужого» сопротивления

Для данной схемы токи $ \underline{I}_{1} $ и $ \underline{I}_{2} $ будут определяться по формулам

$$ {{\underline{I}}_{1}}=\underline{I}\cdot \frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

$$ {{\underline{I}}_{2}}=\underline{I}\cdot \frac{{{\underline{Z}}_{1}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

т.е. ток в одной из параллельных ветвей равен току, подводимому к параллельным ветвям, умноженному на сопротивление «чужой» ветви, и поделённому на сумму сопротивлений параллельных ветвей.

Для более сложного случая, когда в параллельных ветвях имеются источники ЭДС (рис. 2), формула чужого сопротивления будет записываться в следующем виде:

$$ {{\underline{I}}_{1}}=\frac{\underline{I}\cdot {{\underline{Z}}_{2}}+{{\underline{E}}_{1}}-{{\underline{E}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

$$ {{\underline{I}}_{2}}=\frac{\underline{I}\cdot {{\underline{Z}}_{1}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

т.е. дополнительно учитываются источники ЭДС, расположенные в данных ветвях. Формула справедлива при указанных на рис. 2 направлениях ЭДС.

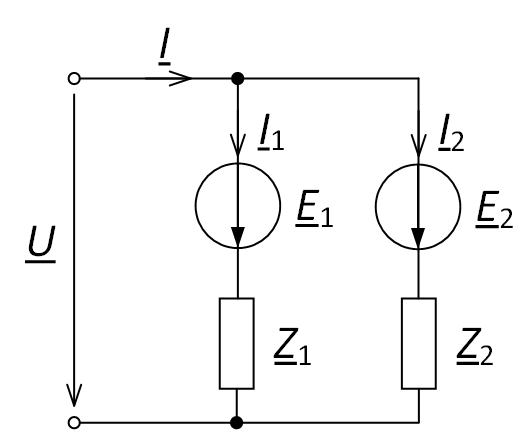
Рис. 2. Схема для определения токов в ветвях по формуле чужого сопротивления при наличии ЭДС

Вывод формул

Выведем формулу чужого сопротивления для схемы по рис. 1.

По закону Ома с учётом параллельного соединения ветвей ток $ \underline{I} $ будет определяться по формуле

$$ \underline{I}=\frac{\underline{U}}{\frac{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}}=\frac{\underline{U}\left( {{\underline{Z}}_{1}}+{{\underline{Z}}_{2}} \right)}{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}. $$

Также по закону Ома

$$ {{\underline{I}}_{1}}=\frac{\underline{U}}{{{\underline{Z}}_{1}}}. $$

Разделим $ \underline{I}_{1} $ на $ \underline{I} $ и получим

$$ \frac{{{\underline{I}}_{1}}}{\underline{I}}=\frac{\frac{\underline{U}}{{{\underline{Z}}_{1}}}}{\frac{\underline{U}\left( {{\underline{Z}}_{1}}+{{\underline{Z}}_{2}} \right)}{{{\underline{Z}}_{1}}\cdot {{\underline{Z}}_{2}}}}=\frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}, $$

откуда

$$ {{\underline{I}}_{1}}=\underline{I}\frac{{{\underline{Z}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Формула для тока $ \underline{I}_{2} $ выводится аналогично.

Выведем формулу чужого сопротивления для схемы по рис. 2.

При выбранных по рис. 2 положительных направлениях тока составим уравнение по первому закону Кирхгофа для узла

$$ \underline{I}={{\underline{I}}_{1}}+{{\underline{I}}_{2}}. $$

По второму закону Кирхгофа

$$ {{\underline{I}}_{2}}\cdot {{\underline{Z}}_{2}}-{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}={{\underline{E}}_{2}}-{{\underline{E}}_{1}}, $$

откуда

$$ {{\underline{I}}_{2}}=\frac{{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}{{{Z}_{2}}}. $$

Разделим $ \underline{I}_{1} $ на $ \underline{I} $ и получим

$$ \frac{{{\underline{I}}_{1}}}{\underline{I}}=\frac{{{\underline{I}}_{1}}}{{{\underline{I}}_{1}}+{{\underline{I}}_{2}}}=\frac{{{\underline{I}}_{1}}}{{{\underline{I}}_{1}}+\frac{{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}{{{Z}_{2}}}}=\frac{{{\underline{I}}_{1}}\cdot {{Z}_{2}}}{{{\underline{I}}_{1}}\cdot {{Z}_{2}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}}. $$

Произведём преобразования, сократив $ \underline{I}_{1} $ в левой и правой частях, и приведём к следующему виду

$$ {{\underline{I}}_{1}}\cdot {{Z}_{2}}+{{\underline{E}}_{2}}-{{\underline{E}}_{1}}+{{\underline{I}}_{1}}\cdot {{\underline{Z}}_{1}}=\underline{I}\cdot {{Z}_{2}}. $$

Отсюда

$$ {{\underline{I}}_{1}}=\frac{\underline{I}\cdot {{\underline{Z}}_{2}}+{{\underline{E}}_{1}}-{{\underline{E}}_{2}}}{{{\underline{Z}}_{1}}+{{\underline{Z}}_{2}}}. $$

Формула для тока $ \underline{I}_{2} $ выводится аналогично.