Физически симметричные составляющие в электрических цепях не существуют. Симметричные составляющие введены для существенного упрощения расчёта трёхфазных цепей благодаря тому, что математически несимметричную систему трёх произвольных векторов всегда можно заменить двумя симметричными системами векторов и одной системой трёх сонаправленных векторов (рис. 1).
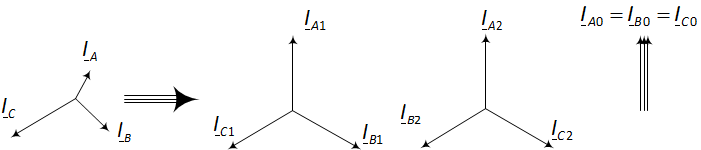
Рис. 1. Преобразование несимметричной системы в набор двух симметричных и одной системы сонаправленных векторов
Далее можно вести расчёт для каждой системы симметричных векторов, представляя трёхфазную схему замещения однолинейной, что на порядок проще, нежели вести расчёт исходной схемы методом контурных токов, по законам Кирхгофа и т.д.
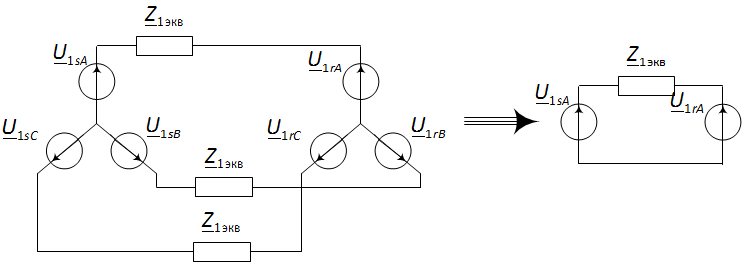
Рис. 2. Расчёт трёхфазной симметричной схемы заменяется расчётом однолинейной схемы для фазы А, величины в других фазах находятся поворотом рассчитанного вектора фазы А на угол 120° или 240°

Воспользуйтесь нашим калькулятором симметричных составляющих.
Не совсем понятно что собственно упрощается: система из 3 векторов заменилась системой из 9 векторов?. Кроме того расчет каждой отдельной схемы также выполняется по тем же законам. Опять возникает тот же вопрос: в чем упрощение?
С тем, что расчёт схемы происходит по тем же законам, не поспоришь. Но почему системой из 9 векторов?
Ладно 9 векторов это я преувеличил: 6 векторов можно получить из остальных 3-х, но вопрос остается 3 вектора — заменили 3 векторами, что упростилось? Помню, что в университете меня так и учили, но на мой взгляд такое объяснение ничего не проясняет. Например, если трехфазный элемент будет полностью «несбалансированным» (матрица сопротивлений этого элемента будет полностью несимметрична), то метод симметричных составляющих не даст никаких преимуществ и никакая замена токов тут не поможет. Если честно рука не поднимается написать, что это камень в огород современной системы образования, ведь даже в знаменитой книге авторов Вагнера и Эванса «Метод симметричных составляющих», которая была написана под идейным руководством самого основоположника метода C.L. Fortescue подход к изложению метода во многом схож с описанным в данной публикации, но это действительно так. И даже несмотря на то, что в указанной выше книге поставлен аналогичный вопрос: «Невольно возникает вопрос, почему разложение трех векторов на девять должно упростить решение задачи?…» ответ на него выглядит совсем не очевидным, хотя он несомненно правилен: «Ответ заключается в том, что результатом разложения являются три системы, из которых каждая является симметричной и может быть рассматриваема отдельно, подобно тому как это делается в симметричных многофазных системах, для которых связанные с ними задачи упрощаются сведением их постоянных и приложенных напряжений к фазовым значениям, а затем решаются как однофазные. В симметричных цепях токи и напряжения различных последовательностей не взаимодействуют друг с другом» ( видимо основную мысль о том, что токи и напряжения различных последовательностей не взаимодействуют друг с другом авторы решили оставить на домысливание самим читателем)
На мой взгляд объяснение «упрощающего эффекта» метода симметричных составляющих надо начинать с рассмотрения свойств симметричных матриц, определением их собственных значений и векторов.
Да, то, что не добавлено упоминание о том, что токи и напряжения различных последовательностей не взаимодействуют друг с другом, является нашим упущением.
да, но опять же повторюсь это утверждение справедливо не для всех случаев (например, если трехфазный элемент «несбалансирован», то метод симметричных составляющих не даст никаких преимуществ). Поэтому важно не только утверждать, что токи и напряжения различных последовательностей не взаимодействуют друг с другом, но и понимать почему.