- Назначение
- Рисование схемы
- Задание параметров
- Методы расчёта
- Баланс мощностей
- Определение показаний амперметров и вольтметров
- Построение векторных диаграмм
- Пользователям
Назначение
Программа предназначена для расчёта установившихся режимов электрических цепей по законам ТОЭ. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта.
Рисование схемы
Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.
В боковой панели доступны следующие элементы с задаваемыми параметрами:
- резистор
 :
:
- номер элемента;
- сопротивление, Ом;
- конденсатор
 :
:
- номер элемента;
- сопротивление, Ом;
- катушка индуктивности
 :
:
- номер элемента;
- сопротивление, Ом;
- источник ЭДС
 :
:
- номер элемента;
- амплитудное значение, В;
- начальная фаза, °;
- источник тока
 :
:
- номер элемента;
- амплитудное значение, А;
- начальная фаза, °.
При наведении указателя мыши на элемент отображаются точки соединения элемента с другими элементами (рис. 1) и кнопка для поворачивания элемента (рис. 2).
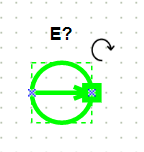
Рис. 1. Точки соединения элемента
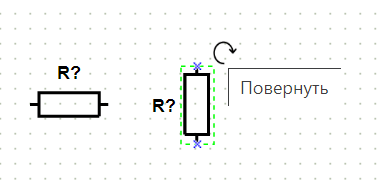
Рис. 2. Кнопка для поворачивания элемента
Для соединения одного элемента с другим необходимо навести указатель мыши на точку соединения элемента, нажать левую клавишу мыши и соединить его с другим элементом (рис. 3), нажав левой клавишей мыши на точке соединения другого элемента.
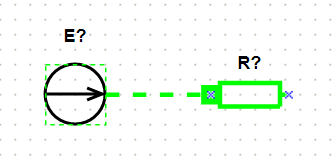
Рис. 3. Соединение элементов
Узлы формируются автоматически при соединении элемента с другой соединительной линией.
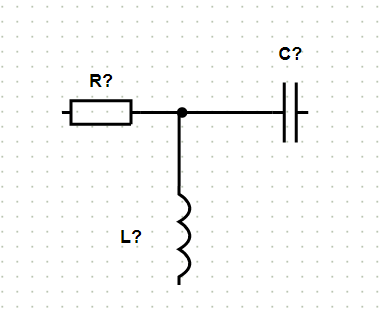
Рис. 4. Формирование узла
При нажатии на элемент в правой части экрана формируется окно с параметрами элемента, которые доступны для редактирования (рис. 5).
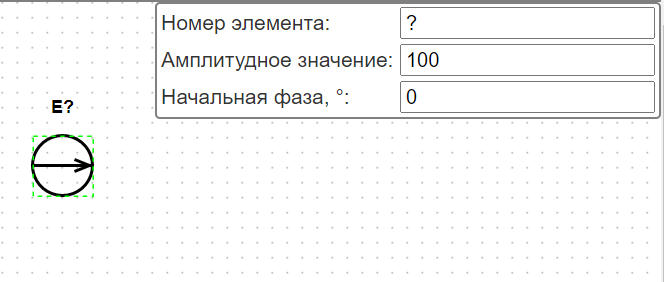
Рис. 5. Задание параметров элемента
Ограничения при рисовании схемы
Для корректного анализа схемы соединительная линия обязательно должна быть соединена с обеих сторон к элементам/соединительным линиям, иначе программа не будет производить расчёт схемы, о чём она просигнализирует соответствующим уведомлением.
Удаление элементов производится нажатием кнопки «Удалить», расположенной в левой части экрана ниже боковой панели с элементами.
Сохранение схемы в виде файла и загрузка схемы из файла
На боковой панели доступна кнопка ![]() для загрузки схемы из файла и кнопка
для загрузки схемы из файла и кнопка ![]() для сохранения исходной схемы в файл.
для сохранения исходной схемы в файл.
Задание параметров
ВНИМАНИЕ! Если параметры элементов задаются в виде вещественного числа, то дробную часть от целой необходимо отделять точкой.
При расчёте можно выбрать единицы измерения, в которых задаются параметры конденсаторов и катушек индуктивности. Доступны 2 варианта:
- Ом
- Ф/Гн
В том случае, если выбран вариант Ф/Гн, необходимо задать частоту. В качестве значения по умолчанию выбрано значение 50 Гц. Частота обязательно должна быть больше нуля.
Если для конденсаторов и катушек индуктивности часть параметров задаётся в Омах, а другая часть — в ёмкостях/индуктивностях, то в этом случае величины необходимо привести к одним. К примеру, сопротивления рассчитываются по известным формулам:
$$ \underline{Z}_{R} = R, $$
$$ \underline{Z}_{L} = jX_{L}, $$
$$ \underline{Z}_{L} = -jX_{C}, $$
где $ X_{L} = \omega L $, $ X_{C} = \frac{1}{\omega C} $, $ R $ – сопротивление резистора, $ L $ – индуктивность катушки, $ C $ – ёмкость конденсатора, $ \omega = 2 \pi f $ – циклическая частота, $ f $ – частота сети, $ j $ – мнимая единица.
Задание параметров источников ЭДС и тока задаются в виде их модуля и фазы. Например, если в исходных данных
$$ \underline{E} = 3 + 4j, $$
то для того, чтобы задать это значение в программу, его необходимо привести в полярную форму. Получим:
$$ \underline{E} = 5 \angle 53.13 \degree $$
Таким образом, в поле «Амплитудное значение» необходимо задать значение 5, а в поле «Начальная фаза» необходимо задать значение 53.13.
Методы расчёта
После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.
Метод расчёта осуществляет путём его выбора в спадающем списке, расположенном ниже кнопки «Расчёт». Приняты следующие обозначения методов:
- ЗК − расчёт по законам Кирхгофа
- МУП − расчёт по методу узловых потенциалов
- МКТ − расчёт по методу контурных токов
- МЭГ − расчёт по методу эквивалентного генератора
- Z − расчёт эквивалентного сопротивления цепи относительно источника питания
Следует обратить внимание на то, что если рассчитываемая схема одноконтурная, то, независимо от выбранного метода расчёта, расчёт будет производиться по закону Ома. Эквивалентное сопротивление цепи может быть рассчитано только для схемы с одним источником питания.
Расчёт по закону Ома
Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
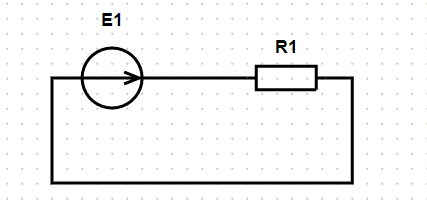
После нажатия кнопки «Расчёт» формируется решение:
В исходной схеме только один контур. Рассчитаем её по закону Ома.
Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ \underline{I} $ направление источника ЭДС $ \underline{E}_{1} $:
$$ R_{1}\cdot \underline{I} = \underline{E}_{1} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ 1.0\cdot \underline{I}=100 $$
Отсюда искомый ток в цепи равен
$$ \underline{I} = 100\space \textrm{А}$$
Расчёт по законам Кирхгофа
Используемая методика при расчёте по законам Кирхгофа приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1
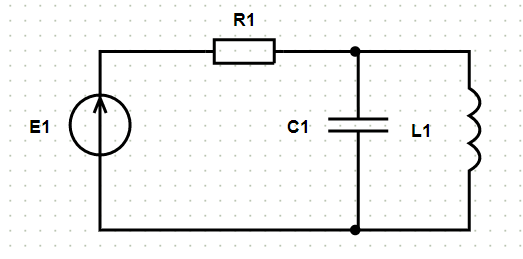
После нажатия кнопки «Расчёт» на исходной схеме отображаются принятые обозначения узлов и принятые направления токов и формируется решение:
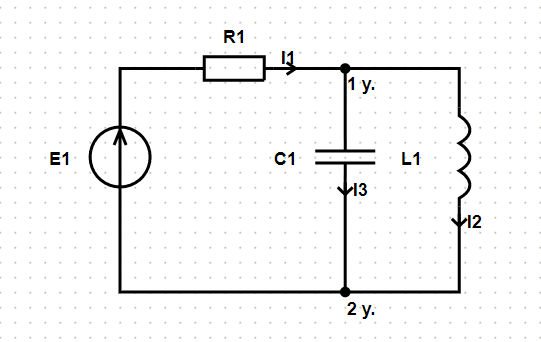
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке.
Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».
Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у} − 1 $, где $ N_\textrm{у} $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.
Составим уравнение для узла №1:
$$ \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0 $$
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.
Составим уравнение для контура №1:
$$ R_{1}\cdot \underline{I}_{1} + jX_{L1}\cdot \underline{I}_{2}=\underline{E}_{1} $$
Составим уравнение для контура №2:
$$ jX_{L1}\cdot \underline{I}_{2}- (-jX_{C1})\cdot \underline{I}_{3}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I}_{1}+jX_{L1}\cdot \underline{I}_{2} = \underline{E}_{1} \\ jX_{L1}\cdot \underline{I}_{2}-(-jX_{C1})\cdot \underline{I}_{3} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}\underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3}=0 \\ \underline{I}_{1}+ j \cdot \underline{I}_{2}=100 \\ j \cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые токи:
$$ \underline{I}_{1} = 0 $$
$$ \underline{I}_{2} =-100j $$
$$ \underline{I}_{3} = 100j $$
Расчёт по методу узловых потенциалов
Используемая методика при расчёте по методу узловых потенциалов приведена здесь.
ВНИМАНИЕ! На данный момент имеются ограничения на расчёт схем по методу узловых потенциалов. Расчёт не производится для больших схем, где имеется большое количество особых ветвей, не связанных между собой. Если расчёт не получается осуществить по методу узловых потенциалов, рекомендуем воспользоваться расчётом по законам Кирхгофа.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» на исходной схеме отображаются принятые обозначения узлов и принятые направления токов и формируется решение:

Рассчитаем схему по методу узловых потенциалов.
В данной схеме: узлов − 2, ветвей − 3, из них особых ветвей − 0. Под особыми ветвями понимаются ветви, в которых имеется только источник ЭДС.
Количество уравнений, составляемых по методу узловых потенциалов, равно $ N_\textrm{у}- 1- N_\textrm{e} $, где $ N_\textrm{у} $ − число узлов, $ N_\textrm{e} $ − число особых ветвей. Для данной схемы количество уравнений, составляемых по методу узловых потенциалов, равно 2 − 1 − 0 = 1.
В исходной схеме нет особых ветвей. Примем потенциал узла №1 равным нулю, т.е. $$ \underline{\varphi}_{1} = 0 \space\textrm{В} $$
Составим уравнения для определения потенциалов остальных узлов.
Уравнение для узла №2:
$$ \underline{\varphi}_{2} \cdot (\frac{1}{R_{1}}+\frac{1}{jX_{L1}}+\frac{1}{-jX_{C1}})-\underline{\varphi}_{1} \cdot \frac{1}{R_{1}}-\underline{\varphi}_{1} \cdot \frac{1}{jX_{L1}}-\underline{\varphi}_{1} \cdot \frac{1}{-jX_{C1}}=- \underline{E}_{1}\cdot \frac{1}{R_{1}} $$
Перенесём все известные слагаемые в правую часть и объединим полученные уравнения в систему. Получим:
$$ \begin{cases} \underline{\varphi}_{2} \cdot (\frac{1}{R_{1}}+\frac{1}{jX_{L1}}+\frac{1}{-jX_{C1}}) = \underline{\varphi}_{1} \cdot \frac{1}{R_{1}}+\underline{\varphi}_{1} \cdot \frac{1}{jX_{L1}}+\underline{\varphi}_{1} \cdot \frac{1}{-jX_{C1}}- \underline{E}_{1}\cdot \frac{1}{R_{1}} \\ \end{cases} $$
Подставим в полученную систему уравнений численные значения и получим:
$$ \begin{cases}\underline{\varphi}_{2}=-100 \\ \end{cases} $$
Решим систему уравнений и получим искомые потенциалы узлов:
$$ \underline{\varphi}_{2} = -100\space\textrm{В} $$
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Определим токи во всех ветвях, кроме особых, по закону Ома для участка цепи:
$$ \underline{I}_{1} = \frac{\underline{\varphi}_{2}- \underline{\varphi}_{1}+ \underline{E}_{1}}{R_{1}}= \frac{(-100)-0+100}{1} =0\space\textrm{А} $$
$$ \underline{I}_{2} = \frac{\underline{\varphi}_{1}- \underline{\varphi}_{2}}{jX_{L1}}= \frac{0-(-100)}{1j} =-100j\space\textrm{А} $$
$$ \underline{I}_{3} = \frac{\underline{\varphi}_{1}- \underline{\varphi}_{2}}{-jX_{C1}}= \frac{0-(-100)}{-1j} =100j\space\textrm{А} $$
Расчёт по методу контурных токов
Используемая методика при расчёте по методу контурных токов приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» на исходной схеме отображаются принятые обозначения узлов и принятые направления токов и формируется решение:

Рассчитаем схему по методу контурных токов.
В данной схеме: узлов − 2, ветвей − 3, независимых контуров − 2.
Количество уравнений, составляемых по методу контурных токов, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей, $ N_\textrm{у} $ − число узлов.
Для данной схемы количество уравнений, составляемых по методу контурных токов, равно 3 − 2 + 1 = 2.
Произвольно зададим направления обхода контуров и соответствующие контурные токи.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{11} $.
Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке. Через эти элементы протекает контурный ток $ \underline{I}_{22} $.
Составим уравнения по методу контурных токов.
Составим уравнение для контура №1:
$$ \underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1}=\underline{E}_{1} $$
Составим уравнение для контура №2:
$$ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми контурными токами. Система уравнений по методу контурных токов для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{11} \cdot (R_{1}+jX_{L1})+\underline{I}_{22} \cdot jX_{L1} = \underline{E}_{1} \\ \underline{I}_{22} \cdot (jX_{L1}- jX_{C1})+\underline{I}_{11} \cdot jX_{L1} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}(1+1j)\cdot \underline{I}_{11}+ j \cdot \underline{I}_{22}=100 \\ j \cdot \underline{I}_{11}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые контурные токи:
$$ \underline{I}_{11} = 0\space\textrm{А} $$
$$ \underline{I}_{22} = -100j\space\textrm{А} $$
Произвольно зададим направления токов в ветвях.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Рассчитаем токи в ветвях исходя из полученных контурных токов.
$$ \underline{I}_{1} =\underline{I}_{11}=0=0 $$ $$ \underline{I}_{2} =\underline{I}_{11}+\underline{I}_{22}=0+(-100j)=-100j $$ $$ \underline{I}_{3} =-\underline{I}_{22}=-(-100j)=100j $$
Расчёт по методу эквивалентного генератора
Суть метода эквивалентного генератора приведена здесь.
Для расчёта тока в ветви по методу эквивалентного генератора необходимо выбрать метод расчёта «МЭГ». После этого необходимо определить все ветви рассчитываемой цепи с помощью кнопки «Ветви» и выбрать ветвь, в которой необходимо рассчитать ток, в полученном спадающем списке.
Для расчёта тока в ветви по методу эквивалентного генератора программа рассчитывает напряжение холостого хода $ \underline{U}_\textrm{хх} $ на выводах разомкнутой ветви с искомым током и внутреннее сопротивление цепи $ \underline{Z}_\textrm{вн} $ относительно ветви с искомым током.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1

После выбора ветви «L1» и нажатия кнопки «Расчёт» на исходной схеме появляется обозначение и направление искомого тока и формируется решение.
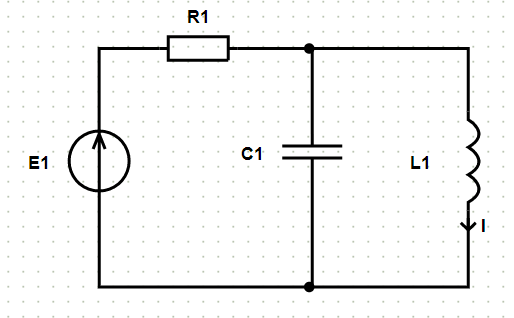
Рассчитаем ток $ \underline{I} $ в ветви с элементами $ L_{1} $ по методу эквивалентного генератора. Для этого рассчитаем напряжение холостого хода на выводах разомкнутой ветви с искомым током и эквивалентное сопротивление пассивной цепи относительно ветви с искомым током.
Рассчитаем напряжение холостого хода. На рисунке ниже приведена рассчитываемая схема. Напряжение холостого хода $ \underline{U}_\textrm{хх} $ сонаправлено с искомым током. Принятое направление искомого тока приведено на схеме выше.
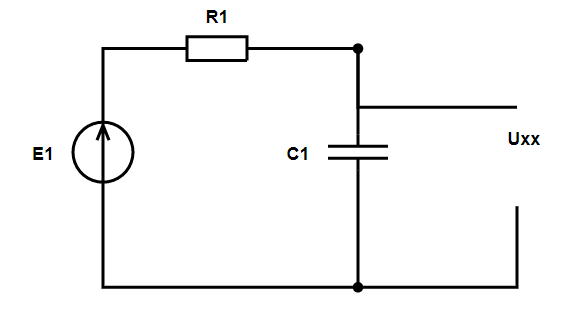
В исходной схеме только один контур. Рассчитаем её по закону Ома.
Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ \underline{I} $ направление источника ЭДС $ \underline{E}_{1} $:
$$ (R_{1}-jX_{C1})\cdot \underline{I} = \underline{E}_{1} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ (1-1j)\cdot \underline{I}=100 $$
Отсюда искомый ток в цепи равен
$$ \underline{I} = 50+50j\space \textrm{А} $$
Определим искомое напряжение холостого хода. Рассмотрим контур, проходящий в указанном порядке через элементы $ \underline{U}_\textrm{хх} $, $ R_{1} $, $ \underline{E}_{1} $, и составим для него уравнение по второму закону Кирхгофа. Получим:
$$ \underline{U}_\textrm{хх}-\underline{I}_{1} \cdot R_{1}=-\underline{E}_{1} $$
Определим напряжение холостого хода. Получим:
$$ \underline{U}_\textrm{хх} = \underline{I}_{1} \cdot R_{1}-\underline{E}_{1}=(50+50j) \cdot 1-100=-50+50j\space\textrm{В} $$
Рассчитаем внутреннее сопротивление цепи $ \underline{Z}_\textrm{вн} $ относительно ветви с искомым током. Для этого из исходной схемы уберём ветвь с искомым током, при этом оставим концы этой ветви. Все источники ЭДС закоротим, а источники тока разомкнем.
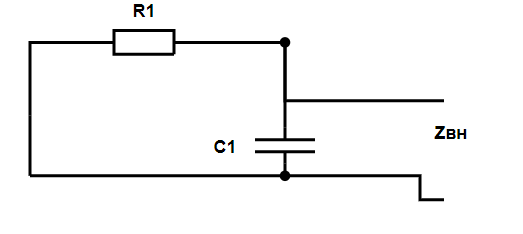
Рассчитаем эквивалентное сопротивление цепи относительно ветви с искомым током.
Ветвь с элементами $ R_{1} $ параллельна ветви с элементами $ C_{1} $. Эквивалентное сопротивление этих ветвей равно:
$$ \underline{Z}_{1} = \frac{R_{1}⋅(- jX_{C1})}{R_{1}- jX_{C1}}=\frac{1⋅(-1j)}{1-1j}=0.5000-0.5000j $$
Внутреннее сопротивление цепи равно:
$$ \underline{Z}_\textrm{вн} = \underline{Z}_{1}+0=0.5000-0.5000j+0=0.5000-0.5000j\space\textrm{Ом} $$
Определим искомый ток:
$$ \underline{I} = \frac{\underline{U}_\textrm{хх}}{\underline{Z}_\textrm{вн}+jX_{L1}} = \frac{-50+50j}{0.5000-0.5000j+1j} =100j\space\textrm{А} $$
Расчёт эквивалентного сопротивления цепи
Используемые формулы расчёта эквивалентного сопротивления цепи приведены здесь.
Расчёт эквивалентного сопротивления осуществляется только для схем с одним источником питания и относительно зажимов этого источника.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза, °: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 2

После нажатия кнопки «Расчёт» на исходной схеме отображаются принятые обозначения узлов и принятые направления токов и формируется решение:

Рассчитаем эквивалентное сопротивление цепи относительно источника $ \underline{E}_{1} $.
Ветвь с элементами $ L_{1} $ параллельна ветви с элементами $ C_{1} $. Эквивалентное сопротивление этих ветвей равно:
$$ \underline{Z}_{1} = \frac{jX_{L1}⋅(- jX_{C1})}{jX_{L1}- jX_{C1}}=\frac{1j⋅(-2j)}{1j-2j}=2j $$
Эквивалентное сопротивление цепи равно:
$$ \underline{Z}_\textrm{экв} = \underline{Z}_{1}+R_{1}=2j+1=1+2j $$
Баланс мощностей
После завершения расчёта программа осуществляет проверку баланса мощностей. Мощности рассчитываются согласно формулам, приведённым здесь.
Пример расчёта баланса мощностей
Рассмотрим расчёт баланса мощностей для схемы, использованной при расчёте по законам Кирхгофа, методу узловых потенциалов и методу контурных токов.
Проверим баланс мощностей.
Определим мощность, потребляемую приёмниками:
$$ \underline{S}_\textrm{пр} = R_{1}⋅|\underline{I}_{1}|^{2}+jX_{L1}⋅|\underline{I}_{2}|^{2}- jX_{C1}⋅|\underline{I}_{3}|^{2}.$$
Подставим числовые значения и получим:
$$ \underline{S}_\textrm{пр} = 1⋅0^2+1j⋅((-100)^{2})-1j⋅(100^{2})=0.$$
Определим мощность, отдаваемую источниками:
$$ \underline{S}_\textrm{ист} = \underline{S}_{\underline{E}} + \underline{S}_{\underline{J}}$$
где $ \underline{S}_{\underline{E}} $ − мощность, отдаваемая источниками ЭДС, $ \underline{S}_{J} $ − мощность, отдаваемая источниками тока.
Определим мощность $ \underline{S}_{\underline{E}} $, отдаваемую источниками ЭДС:
$$ \underline{S}_{\underline{E}} =\underline{E}_{1} ⋅ \underline{I}’_{1}, $$
где $ \underline{I}’ $ означает сопряжённый комплексный ток.
Подставим числовые значения и получим:
$$ \underline{S}_\textrm{\underline{E}} = 100⋅0=0. $$
Т.к. в схеме нет источников тока, то $ \underline{S}_{\underline{J}} = 0. $
Мощность, отдаваемая источниками, равна:
$$ \underline{S}_\textrm{ист} = \underline{S}_{\underline{E}} + \underline{S}_{\underline{J}} =0+0=0. $$
Итак, $ \underline{S}_\textrm{пр} = 0 $, $ \underline{S}_\textrm{ист} = 0 $. Баланс мощностей сходится.
Определение показаний амперметров и вольтметров
Определение показаний измерительных приборов программа позволяет производить в ручном режиме. Для этого необходимо рассчитать схему и определить токи в ветвях.
Показание амперметра определяется как амплитудное значение тока. Рассмотрим расчёт показаний амперметра для схемы, использованной при расчёте по законам Кирхгофа, методу узловых потенциалов и методу контурных токов. В результате расчёта были получены следующие токи:
$$ \underline{I}_{1} = 0 $$
$$ \underline{I}_{2} =-100j $$
$$ \underline{I}_{3} = 100j $$
При установке амперметров в эти ветви ток, измеряемый амперметрами, будет определяться следующим образом:
$$ {I}_{A1} = 0 $$
$$ {I}_{A2} = \sqrt{(\textrm{Re}(\underline{I}_{2}))^2 + (\textrm{Im}(\underline{I}_{2}))^2} = \sqrt{(0)^2 + (-100)^2} = 100\space\textrm{А} $$
$$ {I}_{A3} = \sqrt{(\textrm{Re}(\underline{I}_{3}))^2 + (\textrm{Im}(\underline{I}_{3}))^2} = \sqrt{(0)^2 + (100)^2} = 100\space\textrm{А} $$
Для определения показаний вольтметра необходимо определить напряжение на тех элементах, для которых определяется показание прибора. Для этого необходимо составить уравнение по второму закону Кирхгофа или по закону Ома. Рассчитаем напряжения на элементах $ R_{1} $, $ L_{1} $, $ C_{1} $:
$$ \underline{U}_{R1} = \underline{I}_{1} \cdot R_{1} = 0 \cdot 1 = 0 $$
$$ \underline{U}_{L1} = \underline{I}_{2} \cdot jX_{L1} =-100j \cdot 1j = 100 $$
$$ \underline{U}_{C1} = \underline{I}_{3} \cdot jX_{C1} = 100j \cdot (-1j) = 100 $$
Показания вольтметров определяются следующим образом:
$$ {V}_{R1} = \sqrt{(\textrm{Re}(\underline{U}_{R1})^2 + (\textrm{Im}(\underline{U}_{R1})^2} = \sqrt{0^2 + 0^2} = 0\space\textrm{В} $$
$$ {V}_{L1} = \sqrt{(\textrm{Re}(\underline{U}_{L1})^2 + (\textrm{Im}(\underline{U}_{L1})^2} = \sqrt{100^2 + 0^2} = 100\space\textrm{В} $$
$$ {V}_{C1} = \sqrt{(\textrm{Re}(\underline{U}_{C1})^2 + (\textrm{Im}(\underline{U}_{C1})^2} = \sqrt{100^2 + 0^2} = 100\space\textrm{В} $$
Построение векторных диаграмм
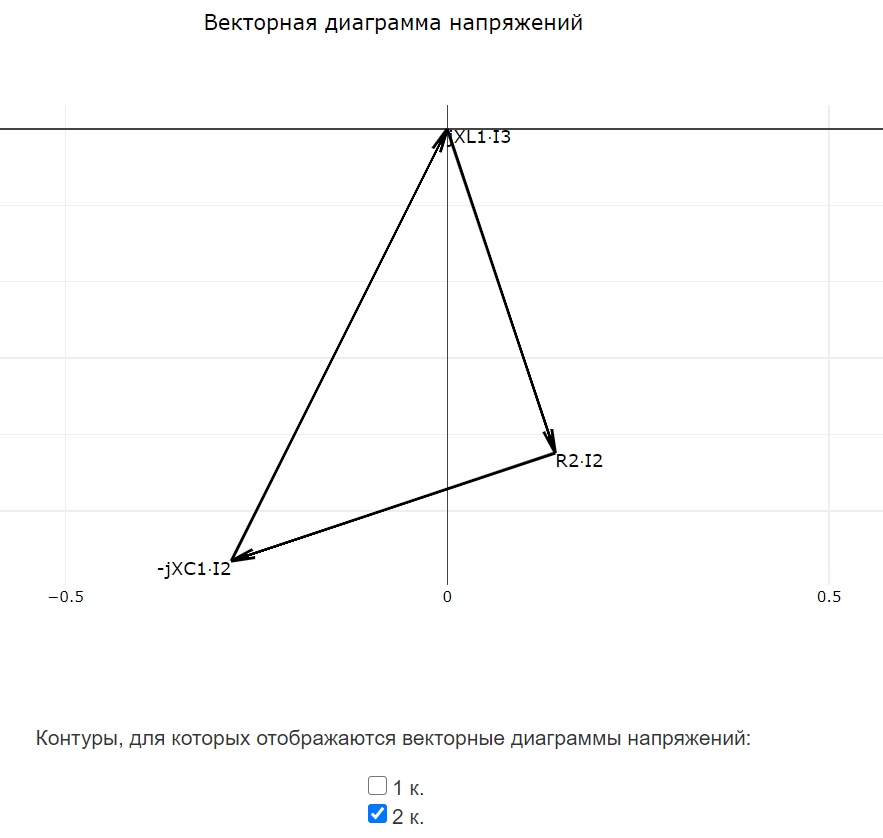
Для цепей, содержащих реактивные элементы (катушки индуктивностей и конденсаторы), после завершения расчёта программа автоматически формирует векторные диаграммы токов и напряжений. Векторные диаграммы строятся согласно методике, приведённой здесь. Векторные диаграммы токов доступны только для многоконтурных схем.
Все векторные диаграммы токов и все векторные диаграммы напряжений строятся на своих графиках. Внизу каждого графика доступны чекбоксы для отображения или скрытия векторных диаграмм для определённых узлов или контуров.
Пример векторных диаграмм токов и напряжений
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 45
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- R2:
- Номер элемента: 1
- Сопротивление, Ом: 1
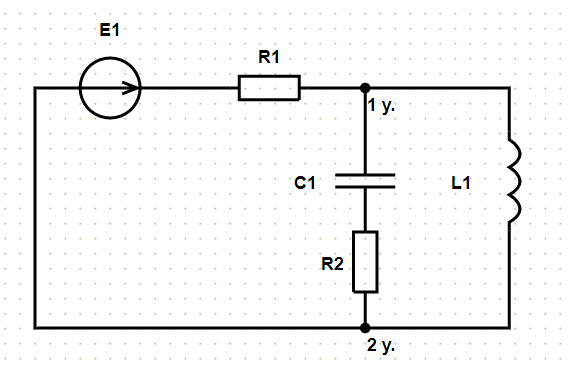
После нажатия кнопки «Расчёт» формируется решение задачи:
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов − 2, ветвей − 3, независимых контуров − 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ R_{2} $, $ C_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ C_{1} $ в указанном порядке.
Контур №2 обходится через элементы $ R_{2} $, $ C_{1} $, $ L_{1} $ в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».
Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у}- 1 $, где $ N_\textrm{у} $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.
Составим уравнение для узла №1:
$$ \underline{I}_{1} + \underline{I}_{2}- \underline{I}_{3} = 0 $$
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.
Составим уравнение для контура №1:
$$ R_{1}\cdot \underline{I}_{1}-(R_{2}-jX_{C1})\cdot \underline{I}_{2}=\underline{E}_{1}$$
Составим уравнение для контура №2:
$$ (R_{2}-jX_{C1})\cdot \underline{I}_{2}+jX_{L1}\cdot \underline{I}_{3}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{1} + \underline{I}_{2}- \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I}_{1}-(R_{2}-jX_{C1})\cdot \underline{I}_{2} = \underline{E}_{1} \\ (R_{2}-jX_{C1})\cdot \underline{I}_{2}+jX_{L1}\cdot \underline{I}_{3} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}\underline{I}_{1}+ \underline{I}_{2}- \underline{I}_{3}=0 \\ \underline{I}_{1}+(-1+1j)\cdot \underline{I}_{2}=0.7071+0.7071j \\ (1-1j)\cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые токи:
$$ \underline{I}_{1} = 0.4243+0.1414j\space\textrm{А} $$
$$ \underline{I}_{2} = 0.1414-0.4243j\space\textrm{А} $$
$$ \underline{I}_{3} = 0.5657-0.2828j\space\textrm{А} $$
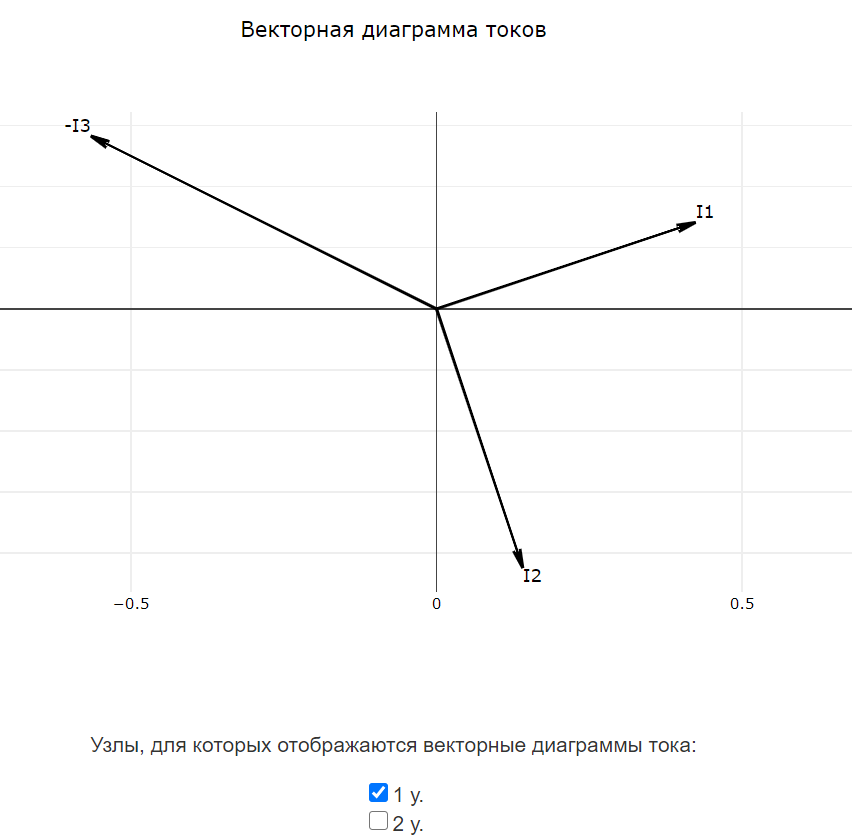
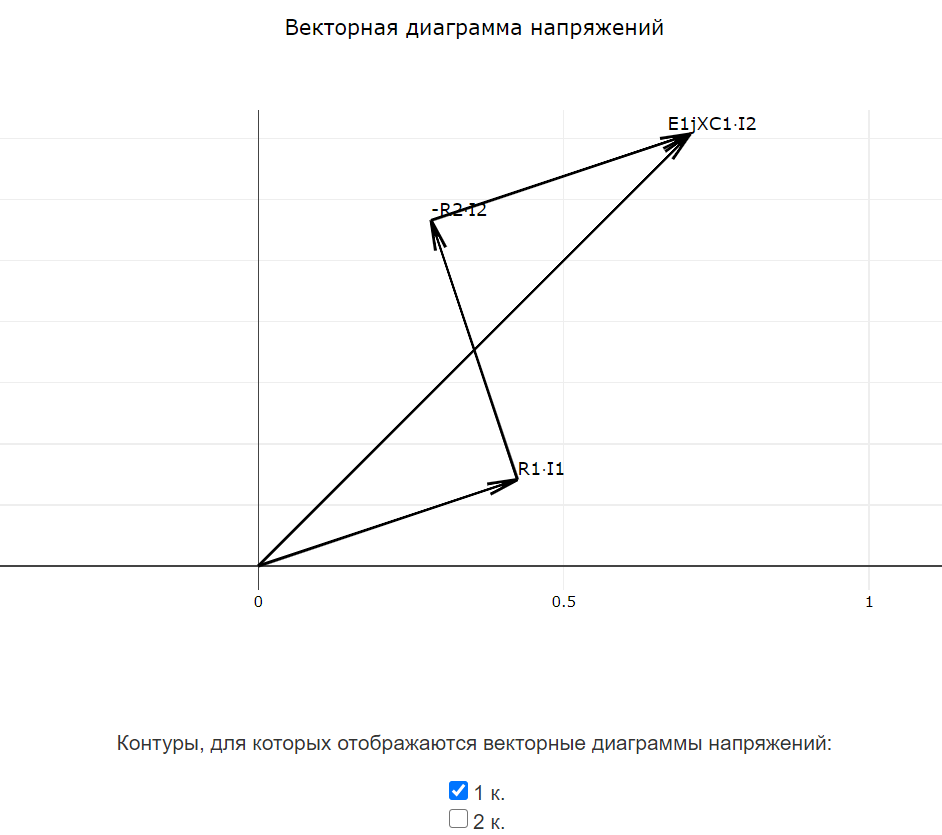
Пользователям
При невозможности рассчитать схему просьба сообщить об этом Администрации сайта по электронной почте support@faultan.ru либо через контактную форму.