При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной диаграммой понимается совокупность векторов, изображающих синусоидальные функции времени [1].
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
- Представление синусоидальных функций в виде комплексных чисел
- Закон Ома в комплексной форме
- Векторная диаграмма при последовательном соединении элементов
- Векторная диаграмма при параллельном соединении элементов
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
$$ i(t) = 10 \sin(\omega t + 30 \degree). $$
Данный синусоидальный сигнал можно представить в виде комплексной величины

$$ \underline{I} = 10 \angle 30 \degree. $$
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Закон Ома в комплексной форме
Известно [1], что напряжение $ \underline{U} $ на сопротивлении $ \underline{Z} $ связано с током $ \underline{I} $, протекающим через это сопротивление, согласно закону Ома:
$$ \underline{U} = \underline{Z} \cdot \underline{I}. $$
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
$$ \underline{Z}_{R} = R, $$
$$ \underline{Z}_{L} = jX_{L}, $$
$$ \underline{Z}_{L} = -jX_{C}, $$
где $ X_{L} = \omega L $, $ X_{C} = \frac{1}{\omega C} $, $ R $ – сопротивление резистора, $ L $ – индуктивность катушки, $ C $ – ёмкость конденсатора, $ \omega = 2 \pi f $ – циклическая частота, $ f $ – частота сети, $ j $ – мнимая единица.
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.
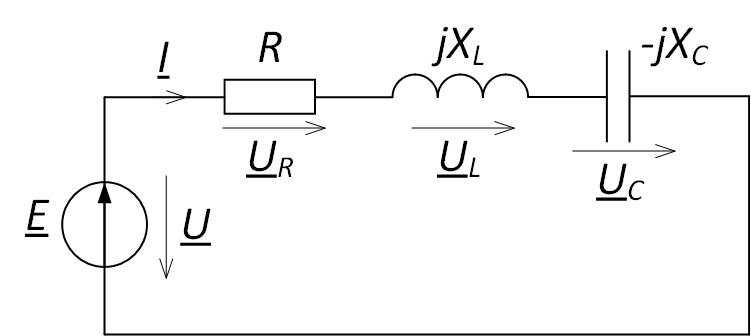 Рис. 1. Последовательное соединение элементов цепи
Рис. 1. Последовательное соединение элементов цепи
Составим уравнение для данной цепи по второму закону Кирхгофа:
$$ \underline{U}_{R} + \underline{U}_{L} + \underline{U}_{C} = \underline{E}. $$
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
$$ \underline{U}_{R} = \underline{I} \cdot R, $$
$$ \underline{U}_{L} = \underline{I} \cdot jX_{L}, $$
$$ \underline{U}_{C} = -\underline{I} \cdot jX_{C}. $$
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что $ j = 1 \angle 90 \degree $, $ -j = 1 \angle -90 \degree $. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу $ j $ приводит к повороту этого вектора на 90° против часовой стрелки, а умножение на $ -j $ приводит к повороту этого вектора на 90° по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока $ \underline{I} $, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе $ \underline{U}_{R} $ совпадает по направлению с током $ \underline{I} $ (т.к. $ \underline{U}_{R} = \underline{I} \cdot R $, а $ R $ – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. $ \underline{U}_{L} = \underline{I} \cdot jX_{L} $, а умножение на $ j $ приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. $ \underline{U}_{C} = -\underline{I} \cdot jX_{C} $, а умножение на $ -j $ приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.
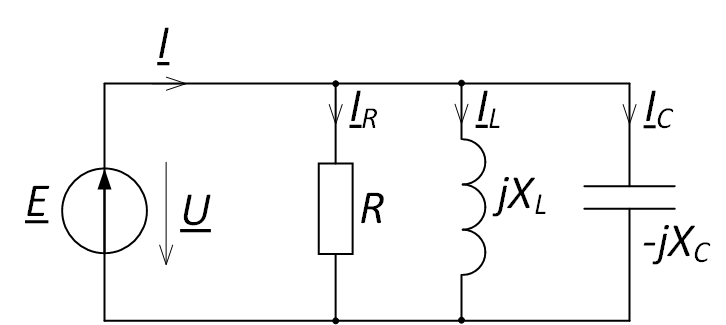
Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа:
$$ \underline{I}- \underline{I}_{R}- \underline{I}_{L}- \underline{I}_{C} = 0, $$
откуда
$$ \underline{I} = \underline{I}_{R} + \underline{I}_{L} + \underline{I}_{C} = 0. $$
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что $ \frac{1}{j} = -j $:
$$ \underline{I}_{R} = \frac{\underline{E}}{R}, $$
$$ \underline{I}_{L} = \frac{\underline{E}}{jX_{L}} = -j \frac{\underline{E}}{X_{L}}, $$
$$ \underline{I}_{C} = \frac{\underline{E}}{-jX_{C}} = j \frac{\underline{E}}{X_{C}}. $$
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС $ \underline{E} $, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС $ \underline{E} $ (т.к. $ \underline{I}_{R} = \frac{\underline{E}}{R} $, а $ R $ – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. $ \underline{I}_{L} = -j \frac{\underline{E}}{X_{L}} $, а умножение на $ -j $ приводит повороту этого вектора на 90° по часовой стрелке). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. $ \underline{I}_{C} = j \frac{\underline{E}}{X_{C}} $, а умножение на $ j $ приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.
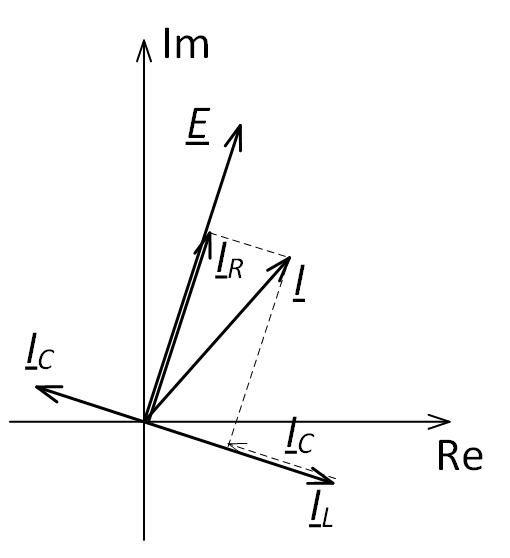
Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Здравствуйте, а как к примеру переводить число в декартовую систему координат, если значение выглядит так: 120e^(j30°)?
Для того, чтобы перевести комплексное число из полярной формы в ортогональную, его необходимо пересчитать следующим образом:
$ 120 e^{j30°} = 120 \cdot \cos(30°) + 120j \cdot \cos(30°) = 103.92 + 60j $