При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов позволяет уменьшить количество решаемых уравнений.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
В методе контурных токов уравнения составляются на основании второго закона Кирхгофа, причём их равно $ N_{\textrm{в}}-N_{\textrm{у}}+1 $, где $ N_{\textrm{у}} $ – число узлов, $ N_{\textrm{в}} $ – число ветвей, т.е. количество совпадает с количеством уравнений, составляемых по второму закону Кирхгофа.
Опишем методику составления уравнений по методу контурных токов. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
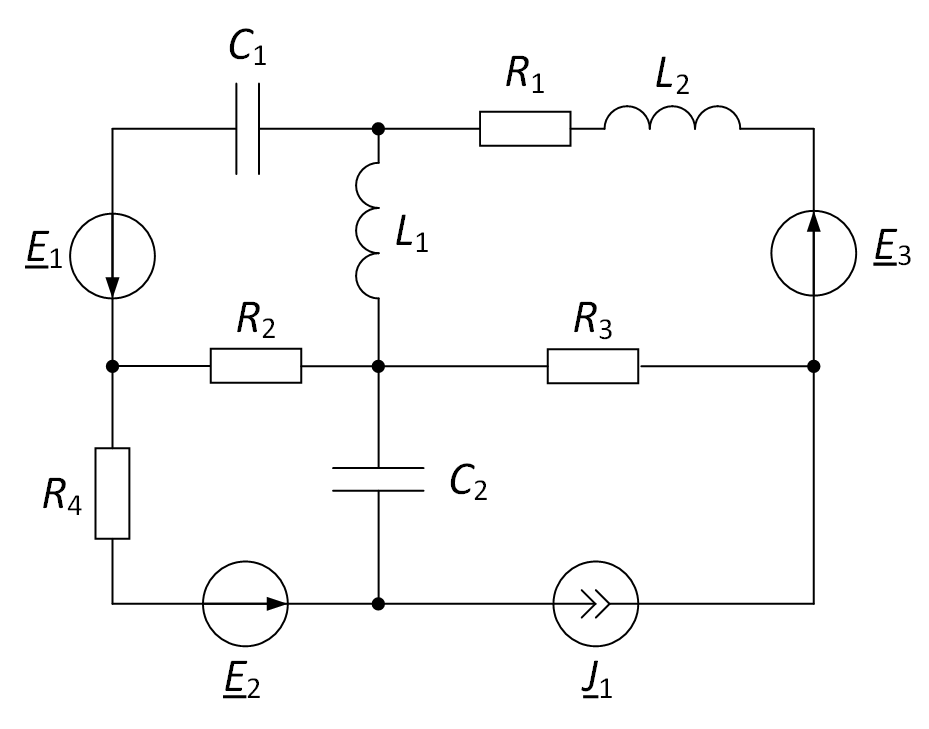
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно направления контурных токов (рис. 2).

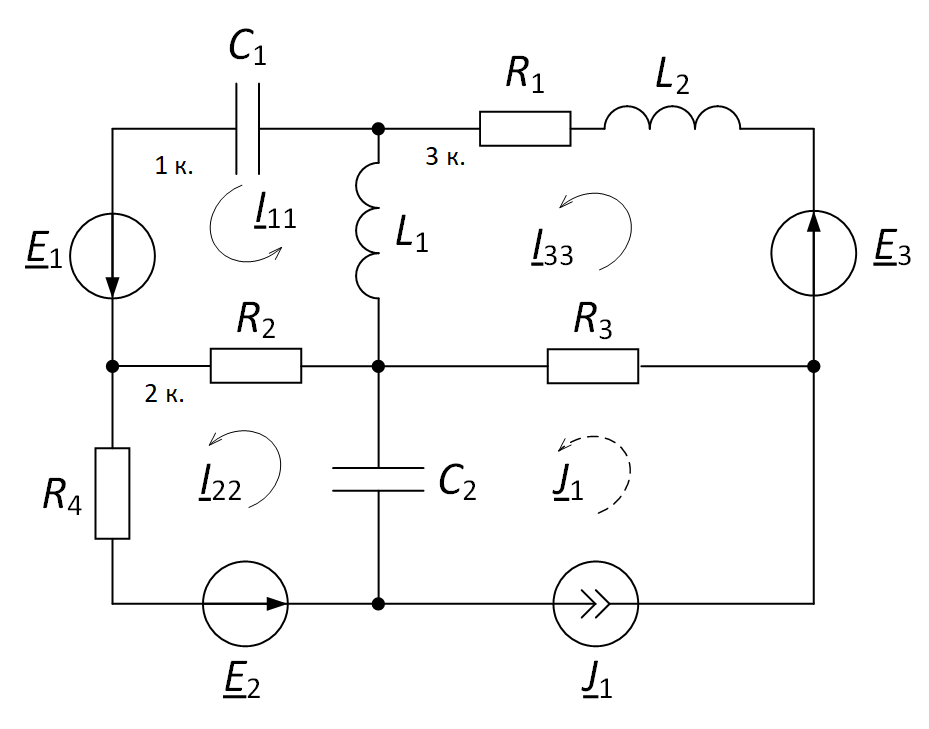
Рис. 2. Задание направления контурных токов в электрической цепи
Количество уравнений, составляемых по методу контурных токов, равно 3. Здесь контур с источником тока так же не рассматривается.
Составим уравнение для контура «1 к.». В контуре «1 к.» контурный ток $ \underline{I}_{11} $ протекает по всем сопротивлениям $ R_{2} $, $ \underline{Z}_{L1} $, $ \underline{Z}_{C1} $. Кроме того, через сопротивление $ R_{2} $ протекает контурный ток смежного контура «2 к.» $ \underline{I}_{22} $, причём контурные токи $ \underline{I}_{11} $ и $ \underline{I}_{22} $ протекают в противоположных направлениях. Через индуктивное сопротивление $ \underline{Z}_{L1} $ также протекает контурный ток $ \underline{I}_{33} $, причём контурные токи $ \underline{I}_{11} $ и $ \underline{I}_{33} $ также протекают в противоположных направлениях. Про составлении уравнения нужно сложить все падения напряжения (аналогично второму закону Кирхгофа), при этом необходимо учесть направление контурных токов: если контурные токи смежных контуров протекают в определённой ветви в одном направлении, то падение напряжения в этой ветви необходимо вносить со знаком «+», в противном случае – со знаком «-». Полученная сумма будет равна сумме ЭДС данного контура, при этом ЭДС берётся со знаком «+», если направление контурного тока совпадает с направлением ЭДС, в противном случае – со знаком «-».
Учитывая вышеизложенное, уравнение по методу контурных токов для контура «1 к.» будет выглядеть следующим образом:
$$ (R_{2} + \underline{Z}_{L1} + \underline{Z}_{C1}) \cdot \underline{I}_{11}- R_{2} \cdot \underline{I}_{22}- \underline{Z}_{L1} \cdot \underline{I}_{33} = \underline{E}_{1}. $$
Аналогично составим уравнение для контура «2 к.». Необходимо учесть, что уравнение для контура с источником тока не составляется, но ток от источника тока также необходимо учитывать в уравнение аналогично контурным токам других контуров. Само уравнение будет выглядеть следующим образом:
$$ -R_{2} \cdot \underline{I}_{11} + (R_{2} + R_{4} + \underline{Z}_{C2}) \cdot \underline{I}_{22}- \underline{Z}_{C2} \cdot \underline{J}_{1} = \underline{E}_{2}. $$
Для контура «3 к.»:
$$ -\underline{Z}_{L1} \cdot \underline{I}_{11} + (R_{1} + R_{3} + \underline{Z}_{L1} + \underline{Z}_{L2}) \cdot \underline{I}_{33}- R_{3} \cdot \underline{J}_{1} = \underline{E}_{3}. $$
В приведённых выше уравнениях $ \underline{Z}_{C} = -\frac{1}{\omega C} $, $ \underline{Z}_{L} = \omega L $.
Таким образом, для того, чтобы найти искомые контурные токи, необходимо решить следующую систему уравнений, где слагаемые с силой тока источника тока перенесены в правую часть уравнений:
$$ \begin{cases} (R_{2} + \underline{Z}_{L1} + \underline{Z}_{C1}) \cdot \underline{I}_{11}- R_{2} \cdot \underline{I}_{22}- \underline{Z}_{L1} \cdot \underline{I}_{33} = \underline{E}_{1} \\ -R_{2} \cdot \underline{I}_{11} + (R_{2} + R_{4} + \underline{Z}_{C2}) \cdot \underline{I}_{22} = \underline{E}_{2} + \underline{Z}_{C2} \cdot \underline{J}_{1} \\ -\underline{Z}_{L1} \cdot \underline{I}_{11} + (R_{1} + R_{3} + \underline{Z}_{L1} + \underline{Z}_{L2}) \cdot \underline{I}_{33} = \underline{E}_{3} + R_{3} \cdot \underline{J}_{1} \end{cases} $$
В данном случае это система из 3 уравнений с 3 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
$$ \begin{bmatrix} R_{2} + \underline{Z}_{L1} + \underline{Z}_{C1} & -R_{2} & -\underline{Z}_{L1} \\ -R_{2} & R_{2} + R_{4} + \underline{Z}_{C2} & 0 \\ -\underline{Z}_{L1} & 0 & R_{1} + R_{3} + \underline{Z}_{L1} + \underline{Z}_{L2} \end{bmatrix} \cdot \begin{bmatrix} \underline{I}_{11} \\ \underline{I}_{22} \\ \underline{I}_{33} \end{bmatrix} = \begin{bmatrix} \underline{E}_{1} \\ \underline{E}_{2} + \underline{Z}_{C2} \cdot \underline{J}_{1} \\ \underline{E}_{3} + R_{3} \cdot \underline{J}_{1} \end{bmatrix} $$
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [R2+Zl1+Zc1 -R2 -Zl1;
-R2 R2+R4+Zc2 0;
-Zl1 0 R1+R3+Zl1+Zl2];
>> b = [ E1;
E2 + Zc2*J1;
E2 + R3*J1];
>> I = A\b
В результате получим вектор-столбец $ \underline{\bold{I}} $ токов из трёх элементов, состоящий из искомых контурных токов, при этом
$$ \underline{\bold{I}}(1) = \underline{I}_{11}, \underline{\bold{I}}(2) = \underline{I}_{22}, \underline{\bold{I}}(3) = \underline{I}_{33}. $$
Далее в схеме по рис. 2 расставим направления токов в ветвях (рис. 3).
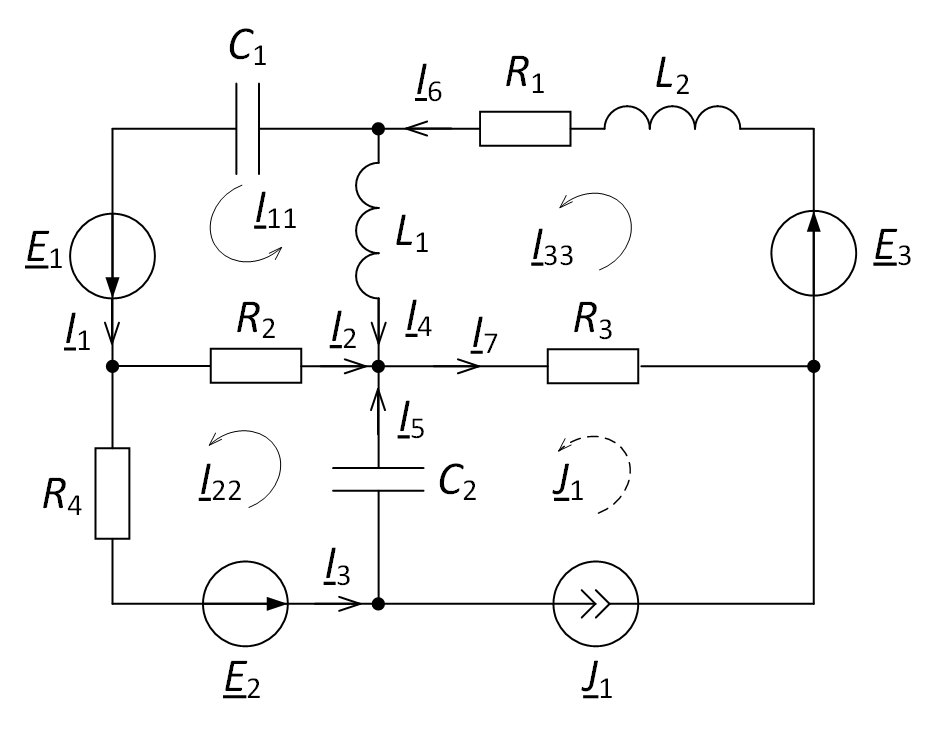
Рис. 3. Задание направления токов в электрической цепи
Для определения токов в ветвях необходимо рассмотреть все контурные токи, которые протекают через данную ветвь. Видим, что через ветвь, где протекает ток $ \underline{I}_{1} $, проходит только один контурный ток $ \underline{I}_{11} $, и он сонаправлен, отсюда
$$ \underline{I}_{1} = \underline{I}_{11}. $$
Через ветвь, где протекает ток $ \underline{I}_{2} $, проходят контурные токи $ \underline{I}_{11} $ и $ \underline{I}_{22} $, причём ток $ \underline{I}_{11} $ совпадает с принятым направлением тока $ \underline{I}_{2} $, а ток $ \underline{I}_{22} $ – не совпадает. Те контурные токи, которые совпадают с принятым направлением, берутся со знаком «+», те, которые не совпадают – со знаком «-». Отсюда
$$ \underline{I}_{2} = \underline{I}_{11}-\underline{I}_{22}. $$
Аналогично для других ветвей
$$ \underline{I}_{3} = \underline{I}_{22}, $$
$$ \underline{I}_{4} =-\underline{I}_{11} + \underline{I}_{33}, $$
$$ \underline{I}_{5} = \underline{I}_{22}- \underline{J}_{1}, $$
$$ \underline{I}_{6} = \underline{I}_{33}, $$
$$ \underline{I}_{7} = \underline{I}_{33}- \underline{J}_{1}, $$
Итак, метод контурных токов позволяет рассчитывать меньшее количество сложных уравнений для расчёта аналогичной электрической цепи по сравнению с законами Кирхгофа.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Написано все правильно, но если честно скучновато.
Отличный повод подготовить статью с интересными фактами по данному методу 😉