Метод фазных координат: пример расчёта матрицы передачи

Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой схемы, которая задаёт взаимосвязь между входными величинами и выходными величинами многополюсника.

Рассмотрим пример расчёта матрицы передачи для схемы на рис. 1.

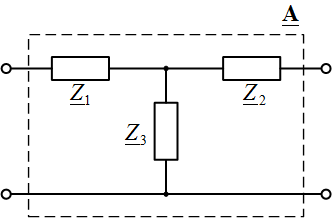Рис. 1. Рассматриваемая схема

Для определения матрицы передачи для рассматриваемой схемы составляются уравнения по законам Кирхгофа. Предварительно обозначают токи и задают произвольно направления токов и напряжений (рис. 2).

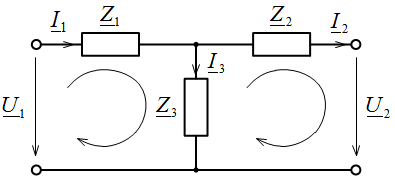
Рис. 2. Задание направлений токов и напряжений

Для схемы составляются уравнения по первому и второму законам Кирхгофа:

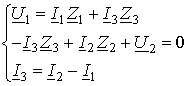
Эти уравнения легко решить с помощью программного комплекса Matlab. Ниже приведён скрипт для расчёта системы уравнений и выделения величин на входе U₁ и I₁ в зависимости от выходных величин для приведённого примера.

>> syms I1 I2 U1 U2 Z1 Z2 Z3
>> I3 = I2-I1;
>> res = solve(U1==I1*Z1+I3*Z3,-I3*Z3+I2*Z2+U2==0,U1,I1);
>> collect(res.U1,U2)
 
ans =
 
(-(Z1 - Z3)/Z3)*U2 + (I2*Z1*Z3 - I2*Z1*Z2 + I2*Z2*Z3)/Z3
 
>> collect(res.I1,U2)
 
ans =
 (-1/Z3)*U2 - (I2*Z2 - I2*Z3)/Z3

Представим полученные уравнения в виде матричного уравнения, связывающего входной ток I₁ и входное напряжение U₁ и выходные параметры многополюсника:

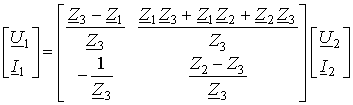
Полученная матрица связи входных и выходных величин называется матрицей прямой передачи многополюсника A. В общем случае уравнение многополюсника формы A записывается в виде

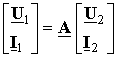
Уравнения формы A применяются в том случае, если многополюсники соединены каскадно (рис. 3).

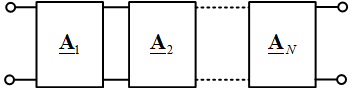
Рис. 3. Каскадное соединение многополюсников

В этом случае эквивалентная матрица прямой передачи всей схемы будет определяться по выражению

A = A₁ ∙ A₂ ∙ … ∙ A_N.

Кроме уравнений формы A широко применяются уравнения формы Y. Эти уравнения применяются в случае параллельного соединения многополюсников (рис. 4).

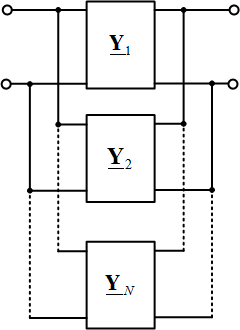
Рис. 4. Параллельное соединение многополюсников

Для такой схемы эквивалентная матрица формы Y будет определяться по формуле

Y = Y₁ + Y₂ + … + Y_N.

Матрица формы A и матрица формы Y связаны между собой. В приложенных файлах приведен пересчёт этих матриц из одной формы в другую на языке Matlab:

• Форма A → Форма Y: файл A_to_Y.m
• Форма Y → Форма A: файл Y_to_A.m