Simulink позволяет осуществлять расчёт установившихся режимов электрических цепей. Для этого используется специальный функционал «Steady-State», предоставляемый блоком powergui.
Пройдите наш онлайн-курс по MATLAB/SIMULINK. Там вы научитесь пользоваться MATLAB как мощным калькулятором, создавать свои модели в SIMULINK, моделировать электрические цепи, а также сложные электроэнергетические системы с устройствами релейной защиты.
Рассмотрим пример расчёта установившегося режима электрической цепи, представленной на рис. 1. Схема в Simulink: checking.mdl. Параметры элементов:
- источник ЭДС E1: амплитуда 5 В, начальная фаза 45°;
- источник тока J1: амплитуда 3 А, начальная фаза 30°;
- резистор R1: сопротивление 2 Ом;
- резистор R2: сопротивление 3 Ом;
- конденсатор C1: сопротивление 2 Ом, что эквивалентно ёмкости, равной 1/(2∙100∙π) Ф;
- катушка индуктивности L1: сопротивление 3 Ом, что эквивалентно индуктивности, равной 3/(100∙π) Гн.
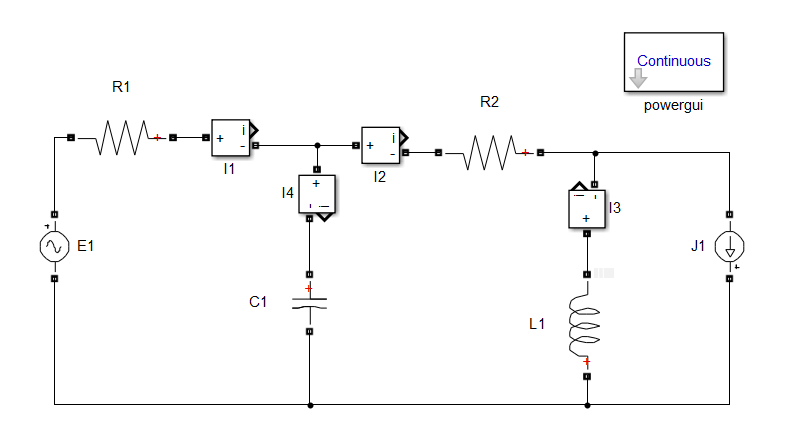
Рис. 1. Рассматриваемая схема
Для того, чтобы рассчитать установившиеся значения токов в ветвях, необходимо в них добавить амперметры, обозначенные на рис. 1 как I1, I2, I3, I4. Принимается, что ток «втекает» в амперметр через зажим «+», то есть положительное направление тока принято от зажима «+» к зажиму «‑» амперметра. Положительное направление источников ЭДС и тока определяется по зажиму «+».
После установки амперметров необходимо перейти в блок powergui, используемый в любой схеме Simulink, где рассчитываются электрические величины. Далее необходимо перейти на вкладку «Tools» и нажать кнопку «Steady-State» (рис. 2).

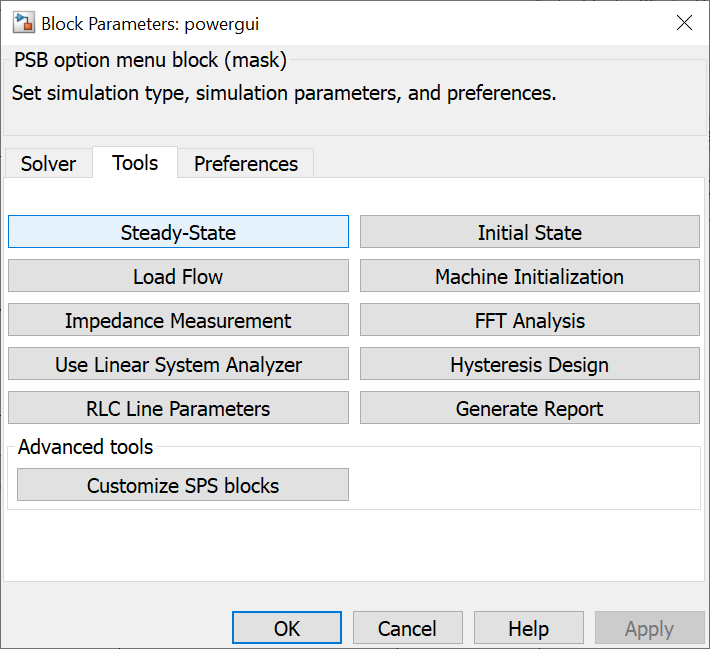
Рис. 2. Функционал «Steady-State» блока powergui
После нажатия кнопки «Steady-State» открывается новое окно (рис. 3), в котором будут отображаться установившиеся значения токов и/или напряжений в полярной форме. В случае каких-либо изменений в исходной схеме для обновления данных необходимо нажать кнопку «Update Steady State Values».
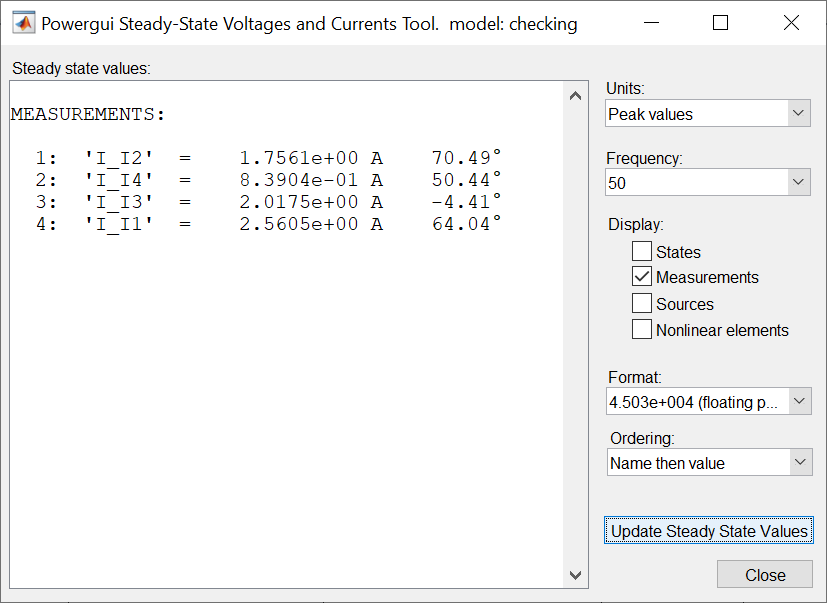
Рис. 3. Отображение установившихся значений электрических величин
Перезапишем полученные значения в ортогональной форме:
$$ \underline{I}_{1} = 2.5605 \angle 64.04 \degree = 1.1208 + j2.3021 $$
$$ \underline{I}_{2} = 1.7561 \angle 70.49 \degree = 0.5865 + j1.6553 $$
$$ \underline{I}_{3} = 2.0175 \angle {-4.41} \degree = 2.0115- j0.1551 $$
$$ \underline{I}_{4} = 8.3904 \angle 50.44 \degree = 0.5344 + j0.6469 $$
В отличие от Simulink, программа онлайн-расчёта электрических цепей позволяет не только рассчитывать токи, она также приводит полный расчёт электрической схемы. После составления схемы, аналогичной схеме по рис. 1, и дальнейшего проведения расчёта программа выводит на экран отображение токов и узлов (рис. 4) и полное решение.
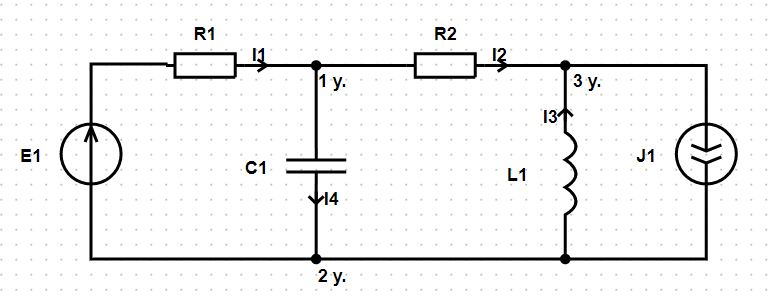
Рис. 4. Отображение положительных направлений токов и номеров узлов
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов – 3, ветвей – 5, независимых контуров – 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
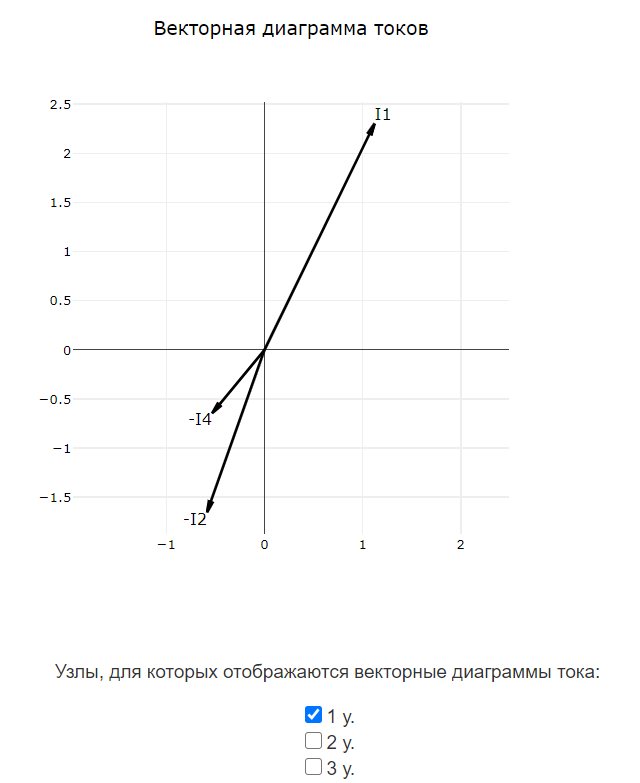
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
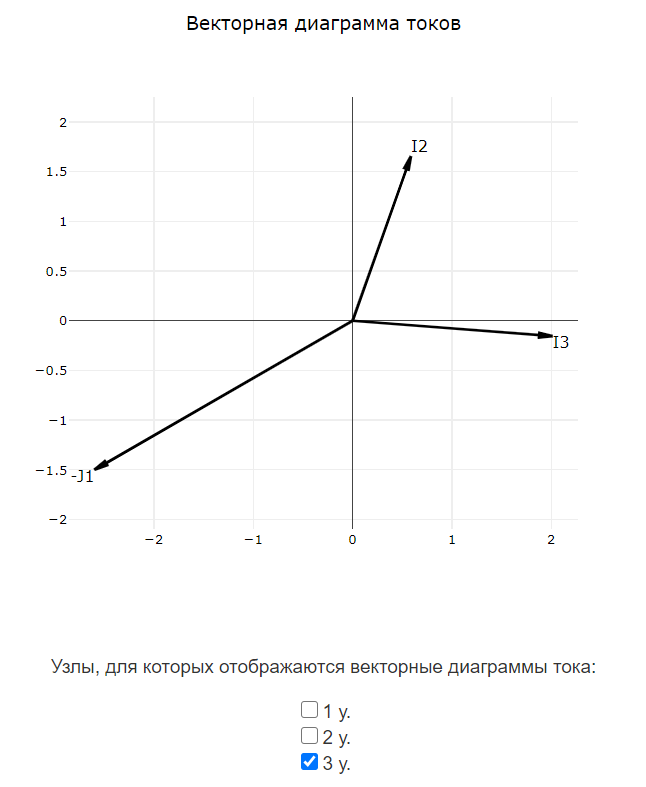
Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘3 у.’ через элементы $ R_{2} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘2 у.’ к узлу ‘3 у.’ через элементы $ L_{1} $.
Ток $ \underline{I}_{4} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ C_{1} $ в указанном порядке.
Контур №2 обходится через элементы $ R_{2} $, $ L_{1} $, $ C_{1} $ в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» – со знаком «‑».
Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у}- 1 $, где $ N_\textrm{у} $ – число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 3 – 1 = 2.
Составим уравнение для узла №1:
$$ \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{4} = 0 $$
Составим уравнение для узла №2:
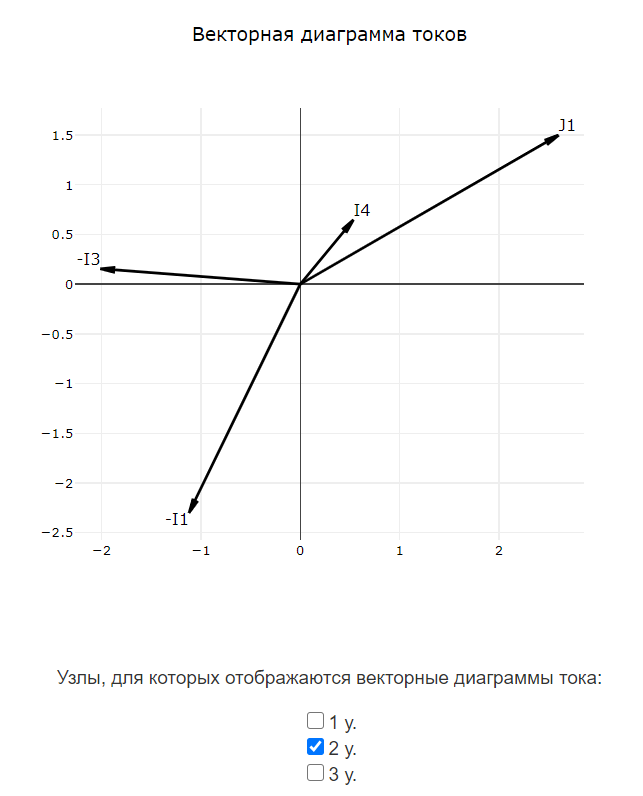
$$ -\underline{I}_{1}- \underline{I}_{3} + \underline{I}_{4} + \underline{J}_{1} = 0 $$
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в}- N_\textrm{у} + 1$, где $ N_\textrm{в} $ – число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 4 – 3 + 1 = 2.
Составим уравнение для контура №1:
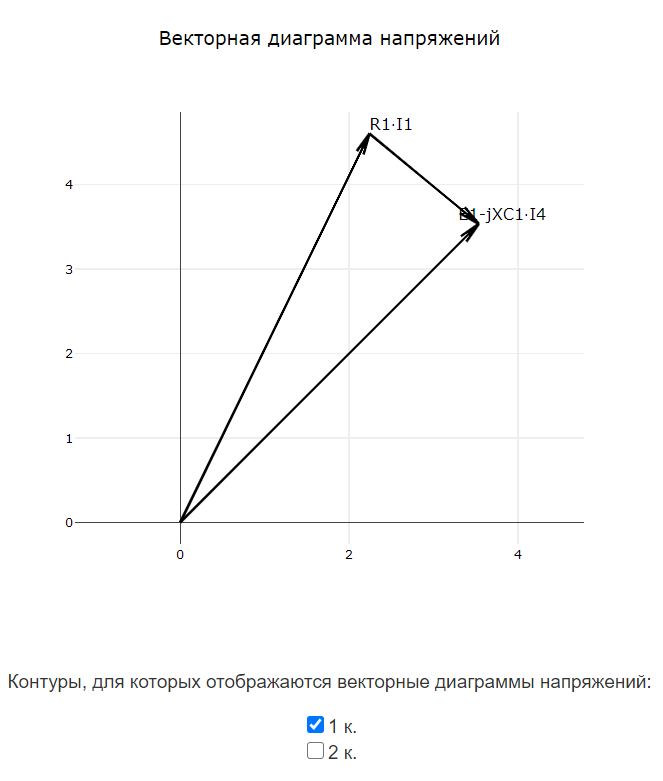
$$ R_{1}\cdot \underline{I}_{1}-jX_{C1}\cdot \underline{I}_{4}=\underline{E}_{1} $$
Составим уравнение для контура №2:
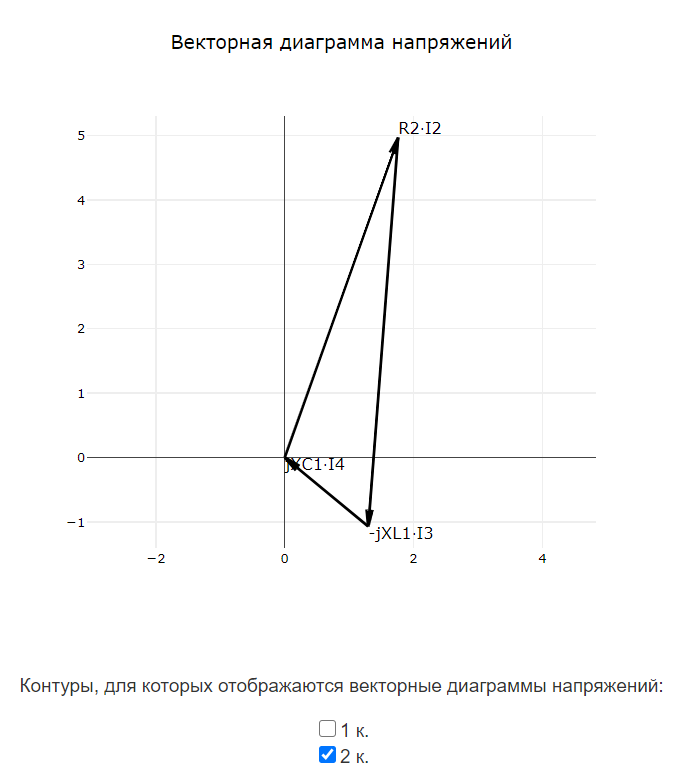
$$ R_{2}\cdot \underline{I}_{2}-jX_{L1}\cdot \underline{I}_{3}-(-jX_{C1})\cdot \underline{I}_{4}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{1}- \underline{I}_{2}- \underline{I}_{4} = 0 \\ -\underline{I}_{1}- \underline{I}_{3} + \underline{I}_{4} = -\underline{J}_{1} \\ R_{1}\cdot \underline{I}_{1}-jX_{C1}\cdot \underline{I}_{4} = \underline{E}_{1} \\ R_{2}\cdot \underline{I}_{2}-jX_{L1}\cdot \underline{I}_{3}-(-jX_{C1})\cdot \underline{I}_{4} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}\underline{I}_{1}- \underline{I}_{2}- \underline{I}_{4}=0 \\ -\underline{I}_{1}- \underline{I}_{3}+ \underline{I}_{4}=-2.5981-1.5000j \\ 2.0\cdot \underline{I}_{1}-2.0j \cdot \underline{I}_{4}=3.5355+3.5355j \\ 3.0\cdot \underline{I}_{2}-3.0j \cdot \underline{I}_{3}+2j\cdot \underline{I}_{4}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые токи:
$$ \underline{I}_{1} = 1.1209+2.3021j\space\textrm{А} $$
$$ \underline{I}_{2} = 0.5865+1.6553j\space\textrm{А} $$
$$ \underline{I}_{3} = 2.0115-0.1553j\space\textrm{А} $$
$$ \underline{I}_{4} = 0.5344+0.6469j\space\textrm{А} $$
Незначительная погрешность в результатах обусловлена низкой точностью отображения углов в блоке powergui Simulink.