Реле сопротивление – ещё один вид реле, используемый в релейной защите. Отличием данного реле является то, что оно является реле с двумя подводимыми величинами, а его срабатывание определяется попаданием входной величины (замера) в некую характеристику срабатывания. Замером в данном случае является комплексное сопротивление Z.
Пройдите наш онлайн-курс по MATLAB/SIMULINK. Там вы научитесь пользоваться MATLAB как мощным калькулятором, создавать свои модели в SIMULINK, моделировать электрические цепи, а также сложные электроэнергетические системы с устройствами релейной защиты.
Выделяют большое количество реле сопротивления с различными характеристиками срабатывания [1]:
- с круговой характеристикой, в том числе со смещением;
- с эллипсовидной характеристикой;
- с полигональной характеристикой и др.
В данной статье рассмотрим пример реализации реле сопротивления с круговой характеристикой со смещением в Simulink. Для начала приведём математическое описание данной характеристики. Сама характеристика приведена на рис. 1. Следует отметить тот факт, что центр характеристики располагается на линии максимальной чувствительности (это линия, проходящая через центр координат под углом максимальной чувствительности jм.ч.).
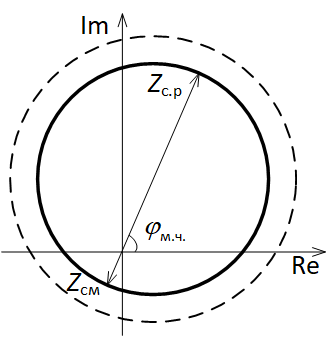
Рис. 1. Вид характеристики реле сопротивления с круговой характеристикой со смещением
Реле сопротивления, в основном, применяется в качестве реле минимального действия. У данного типа реле сопротивления есть несколько уставок:

- уставка срабатывания Zс.р, Ом;
- сопротивление смещения характеристики Zсм, Ом;
- угол максимальной чувствительности φм.ч., градус;
- коэффициент возврата kв, определяющий возврат реле в несработанное состояние (характеристика, указанная на рис. 1 штриховой линией).
Срабатывание реле происходит при попадании замера в характеристику, указанную на рис. 1 сплошной линией, а возврат реле – при последующем уходе замера из характеристики, указанной на рис. 1 штриховой линией. Для определения условий срабатывания реле отметим на характеристике срабатывания центр характеристики Z0 и её радиус R (рис. 2).
Примечание: подчёркивание снизу параметра, например, Z, обозначает, что используется комплексное число.
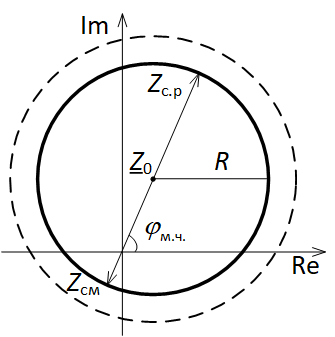
Рис. 2. Характеристика реле сопротивления с указанными центром и радиусом
Срабатывание реле происходит при выполнении условия
![]()
где Z – замер сопротивления на входе реле, Z0 – координата центра характеристики; R – радиус характеристики.
Таким образом, для того, чтобы смоделировать данное реле сопротивления, необходимо определить значение координаты центра характеристики Z0 и значение её радиуса R. Учёт того факта, что центр характеристики располагается на линии максимальной чувствительности, приводит к следующим уравнениям:
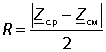
![]()
где значения Zс.р и Zсм определяются по следующим равенствам:
![]()
![]()
где Zс.р, Zсм, φм.ч. – уставки реле.
Возврат реле осуществляется при выходе замера из характеристики срабатывания, которая отличается только большим радиусом при неизменном центра характеристики (рис. 1). Для реализации характеристики возврата достаточно только умножить величину R на коэффициент возврата kв.
Реле сопротивления с круговой характеристикой вы можете приобрести в магазине. Вид схемы приведён на рис. 3. Отметим, что дополнительная логика, такая как учёт тока точной работы реле и др., в данном примере не рассмотрена.
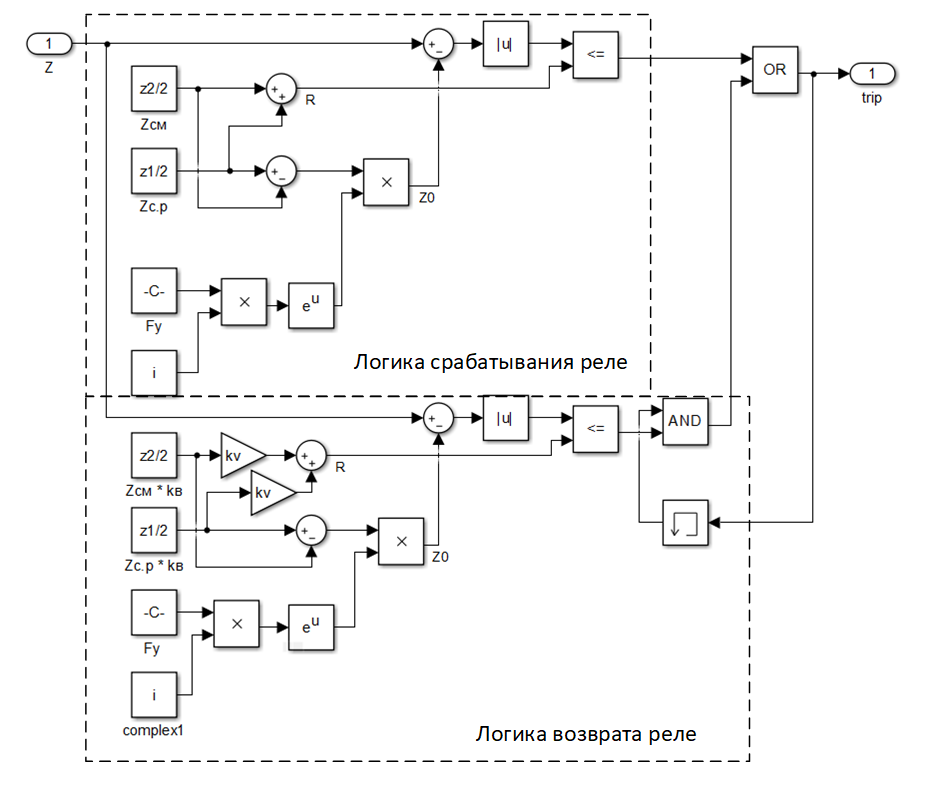
Рис. 3. Реализация реле сопротивления с круговой характеристикой в Simulink
Протестируем данное реле с использованием замера Z, у которого угол постоянный и равен углу максимальной чувствительности. Уставки реле выставлены следующие: Zс.р = 100 Ом, Zсм = 50 Ом, φм.ч. = 75°, kв = 1,05. На рис. 4 приведён вид схемы для тестирования.
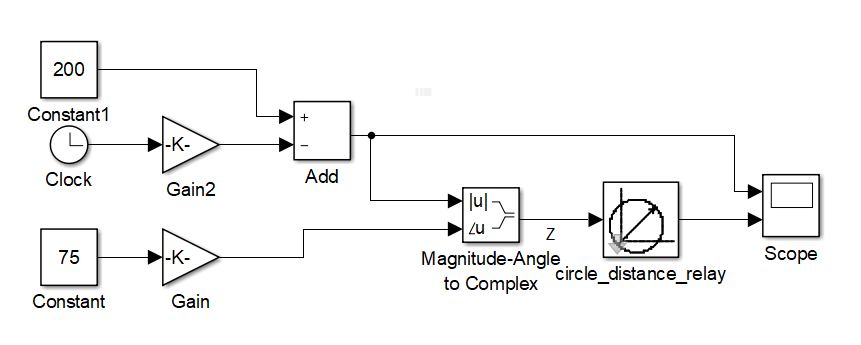
Рис. 4. Схема для тестирования реле сопротивления
На рис. 5 приведён модуль входного замера и результат срабатывания и возврата реле сопротивления.
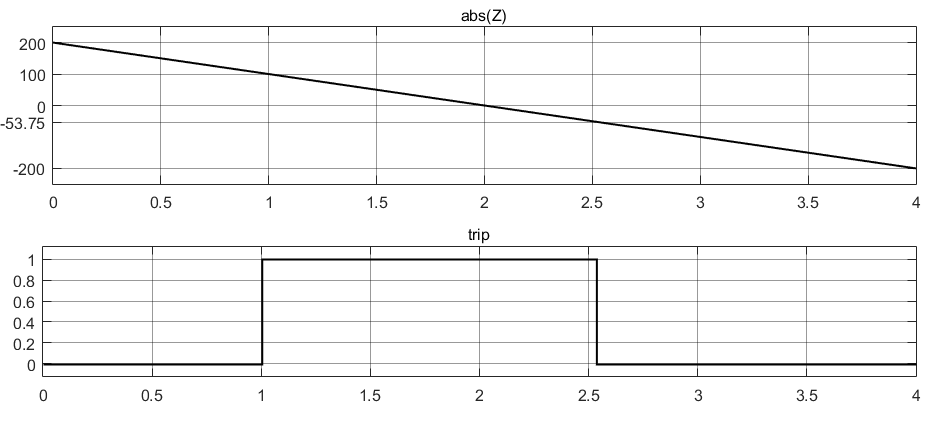
Рис. 5. Результаты тестирования реле сопротивления
Для более подробного тестирования на нашем сайте в дальнейшем дополнительно будет приведён специальный скрипт.
Однако, остаётся открытым вопрос правильности моделирования характеристики возврата реле сопротивления и расчёта самого коэффициента возврата.
Список использованной литературы
- Чернобровов Н.В., Семёнов В.А. Релейная защита энергетических систем. – М.: Энергоатомиздат, 1998.
В Simulink схеме для организации возврата еще и Z0 умножается на Kv, а в тексте предлагается только изменять радиус. Если делать как в тексте то при малых Zсм и больших Zср при измерении Kv в точке Zсм Kv будет много больше единицы. Хорошо это или плохо — не знаю.
Здравствуйте! Спасибо за замечание! Умножение Z0 на коэффициент возврата — излишнее, схему доработаем.
Если измените схему, то при том же тесте возврат будет при -53.75 Ом, что дает Kв = 53.75 / 50 = 1.075.
Сейчас проводим дополнительные исследования. Действительно, задача очень непростая. Для обеспечения одинакового коэффициента возврата при любом угле замера сопротивления центр Z0, похоже, тоже нужно смещать. С другой стороны, насколько это оправдано — не понятно. В документации фирм-производителей устройств РЗА, в учебниках по релейной защите информацию о характеристике возврата не нашли.
После долгого обсуждения с коллегами мы пришли к выводу, что правильнее будет моделировать реле сопротивления именно так, как нарисовано на рис. 1, т.е. смещать Z0 не нужно. Однако вопрос расчёта коэффициента возврата привёл к достаточно обширной дискуссии, в итоге чего мы решили, что коэффициент возврата в данном случае правильнее считать от центра характеристики.
Позиция ясна (интересно, а как в той же ЭПЗ 1636?). По сути, характеристика возврата получается через преобразование подобия с коэффициентом — 1.05. Главное выбрать центр этого преобразования. В одном случае — начало координат, в другом — центр окружности.
Кв теперь получается надо будет считать как |Zвз — Z0| / |Zср — Z0|.
С полигональной характеристикой так лихо не получится. Там «центр» так однозначно не выбрать, особенно если сторон не 4.