В программе онлайн-расчёта электрических цепей появился функционал построения векторных диаграмм.
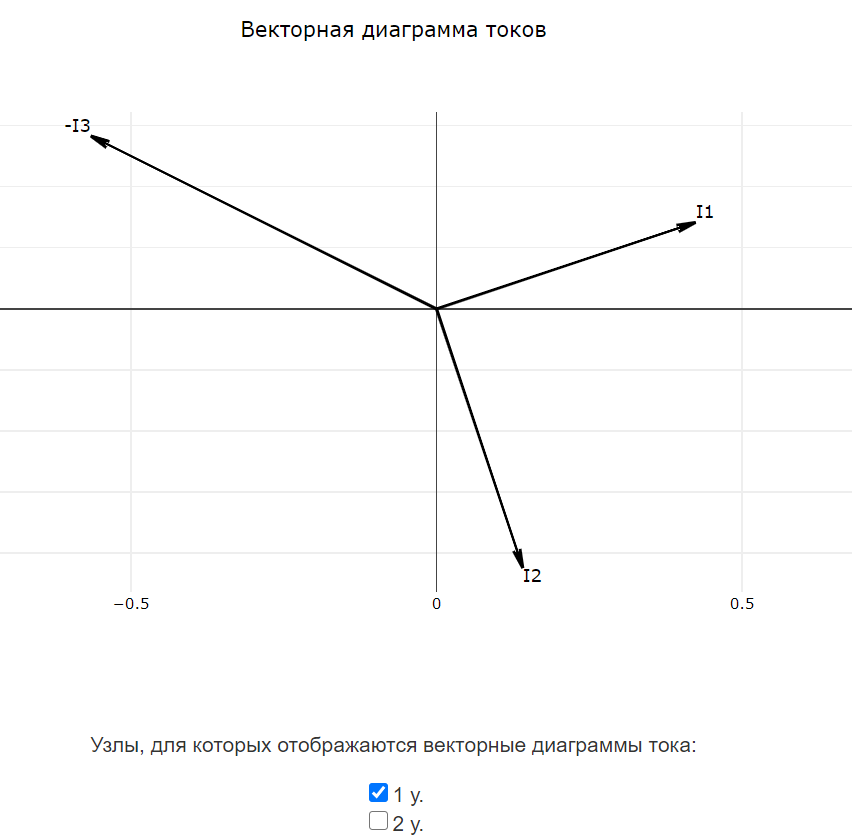
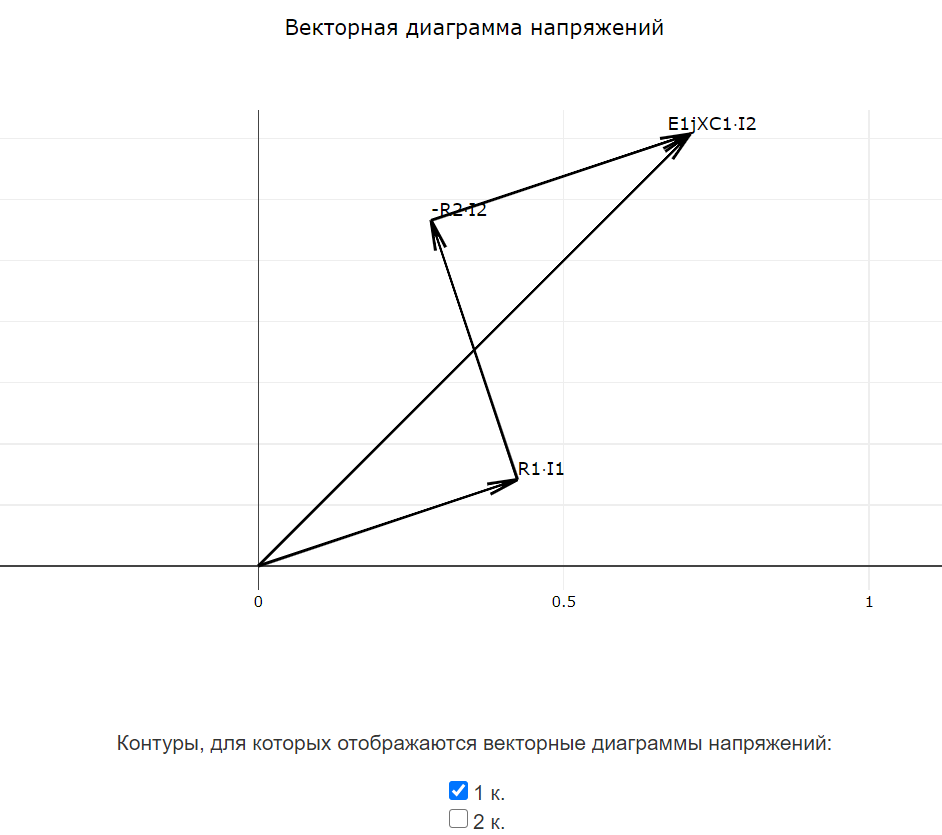
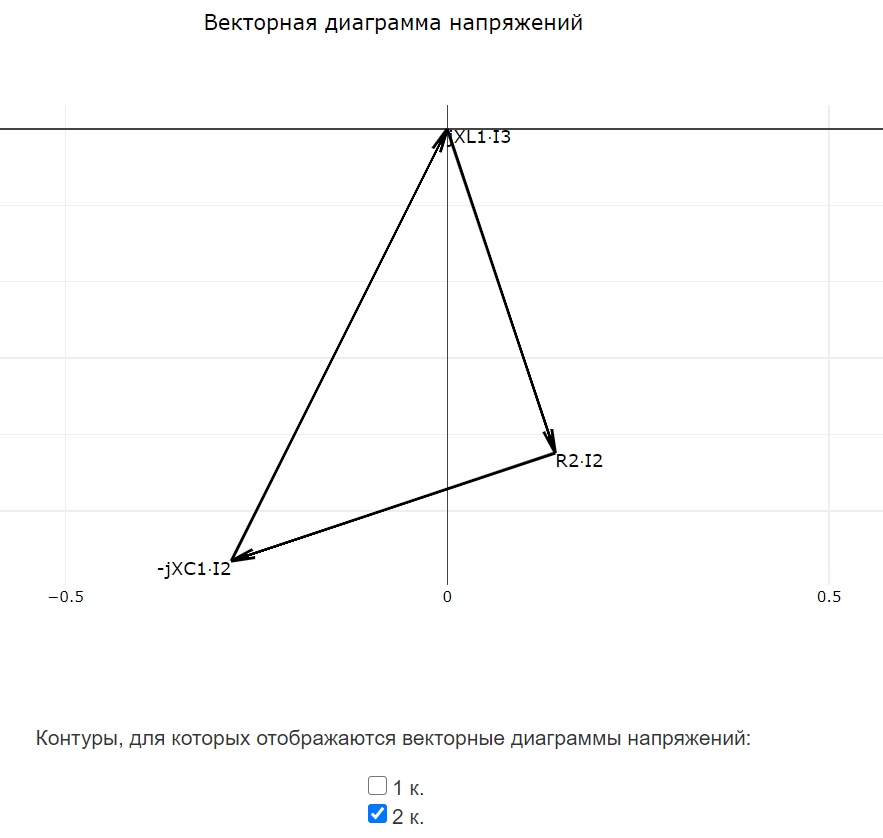
После завершения расчёта программа автоматически формирует векторные диаграммы токов и напряжений. Векторные диаграммы строятся согласно методике, приведённой здесь. Векторные диаграммы токов доступны только для многоконтурных схем.
Все векторные диаграммы токов и все векторные диаграммы напряжений строятся на своих графиках. Внизу каждого графика доступны чекбоксы для отображения или скрытия векторных диаграмм для определённых узлов или контуров.
Пример векторных диаграмм токов и напряжений
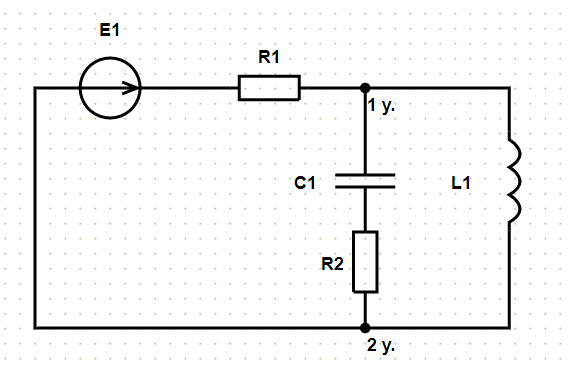
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 45
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- L1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- C1:
- Номер элемента: 1
- Сопротивление, Ом: 1
- R2:
- Номер элемента: 1
- Сопротивление, Ом: 1

После нажатия кнопки «Расчёт» формируется решение задачи:
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов − 2, ветвей − 3, независимых контуров − 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов:
Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $.
Ток $ \underline{I}_{2} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ R_{2} $, $ C_{1} $.
Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $.
Принятые направления обхода контуров:
Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ C_{1} $ в указанном порядке.
Контур №2 обходится через элементы $ R_{2} $, $ C_{1} $, $ L_{1} $ в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».
Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у}- 1 $, где $ N_\textrm{у} $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.
Составим уравнение для узла №1:
$$ \underline{I}_{1} + \underline{I}_{2}- \underline{I}_{3} = 0 $$
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в}- N_\textrm{у} + 1 $, где $ N_\textrm{в} $ − число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.
Составим уравнение для контура №1:
$$ R_{1}\cdot \underline{I}_{1}-(R_{2}-jX_{C1})\cdot \underline{I}_{2}=\underline{E}_{1}$$
Составим уравнение для контура №2:
$$ (R_{2}-jX_{C1})\cdot \underline{I}_{2}+jX_{L1}\cdot \underline{I}_{3}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{1} + \underline{I}_{2}- \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I}_{1}-(R_{2}-jX_{C1})\cdot \underline{I}_{2} = \underline{E}_{1} \\ (R_{2}-jX_{C1})\cdot \underline{I}_{2}+jX_{L1}\cdot \underline{I}_{3} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}\underline{I}_{1}+ \underline{I}_{2}- \underline{I}_{3}=0 \\ \underline{I}_{1}+(-1+1j)\cdot \underline{I}_{2}=0.7071+0.7071j \\ (1-1j)\cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые токи:
$$ \underline{I}_{1} = 0.4243+0.1414j\space\textrm{А} $$
$$ \underline{I}_{2} = 0.1414-0.4243j\space\textrm{А} $$
$$ \underline{I}_{3} = 0.5657-0.2828j\space\textrm{А} $$