Метод фазных координат: пример составления модели сети

Рассмотрим пример составления модели электропередачи с помощью метода фазных координат. На рис. 1 представлена электропередача, математическую модель которой необходимо составить. Необходимо определить токи в режиме короткого замыкания в начале линии.

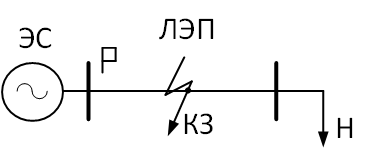Рис. 1. Пример электропередачи

Для различных элементов электропередачи доступны следующие параметры:

1. Энергосистема (ЭС) – ЭДС и сопротивление по прямой и нулевой последовательности;
2. Линия электропередачи (ЛЭП) – длина линии, погонные сопротивления и проводимости;
3. Нагрузка (Н) – мощность нагрузки;
4. Модель повреждения (КЗ) – вид повреждения и переходные сопротивления в повреждённых фазах.

В методе фазных координат исследуемая электропередача будет представлена в виде каскадного соединения многополюсников (рис. 2). На рисунке также указаны искомые токи и напряжения .

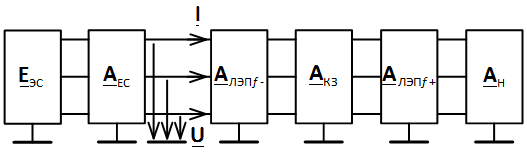
Рис. 2. Исследуемая электропередача, описанная в базисе фазных координат

В Matlab матрицы прямой передачи элементов будут рассчитываться с помощью следующих функций:

• для энергосистемы – функция A_eqsys.m;
• для линии электропередачи от начала до места повреждения – функция A_line;
• для модели повреждения – функция A_fault.m;
• для линии электропередачи от места повреждения до конца линии– функция A_line.m;
• для нагрузки – функция A_load.m.

Для расчёта токов и напряжений в начале линии электропередачи необходимо составить эквивалентную матрицу прямой передачи для схемы:

A = A_ЭС ∙ A_ЛЭПf— ∙ A_КЗ ∙ A_ЛЭПf+ ∙ A_Н.

Исследуемая схема рис. 2 будет представлена эквивалентной схемой (рис. 3).

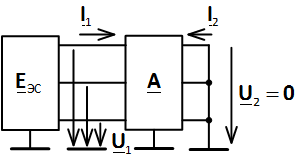
Рис. 3. Эквивалентная схема с матрицей прямой передачи

При расчёте известны ЭДС энергосистемы E_ЭС. Кроме того известно, что напряжения в конце электропередачи за нагрузкой равно нулю (так как там глухозаземлённая нейтраль). Для расчёта токов в начале электропередачи необходимо пересчитать матрицу прямой передачи A в матрицу формы Y с помощью функции A_to_Y.m. В результате схема по рис. 3 может быть представлена в виде схемы с матрицей проводимости (рис. 4).

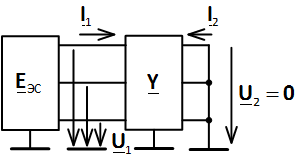
Рис. 4. Эквивалентная схема c матрицей проводимости

Из схемы рис. 4 видно, что 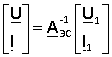. Отсюда можно рассчитать токи:

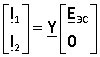
где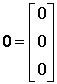

Рассчитав ток I₁, можно рассчитать и искомый ток, и искомое напряжение. Для этого рассмотрим подробнее рис. 2. Обозначим на схеме полученный ток (рис. 5).

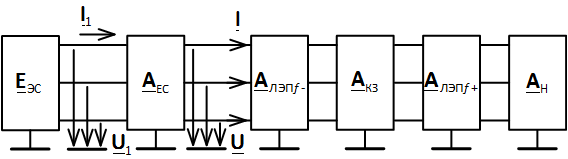
Рис. 5. Исследуемая электропередача, описанная в базисе фазных координат

Как уже было рассказано, матрица формы A связывает токи и напряжения на входе и на выходе многополюсника определённым соотношением. Для схемы рис. 5

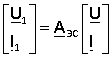
Таким образом, для того, чтобы определить искомые величины, необходимо решить это матричное уравнение. Его решение следующее

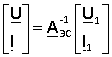
где – обратная матрица для матрицы прямой передачи энергосистемы A_ЭС.

Представленный в заметке расчёт приведён в приложенном файле программы в среде Matlab.