В дополнение к предыдущей статье рассмотрим пример составления модели сети с изолированной нейтралью. Рассмотрим простейшую линию электропередачи с односторонним питанием (рис. 1). Необходимо составить модель электропередачи, которая будет выдавать токи и напряжения в начале линии в режимах коротких замыканий и в режимах однофазного замыкания на землю (ОЗЗ).
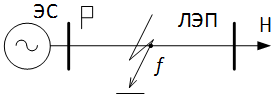
Рис. 1. Рассматриваемая линия электропередачи с изолированной нейтралью
Как уже было написано, основная сложность составления модели сети с изолированной нейтралью состоит в том, что необходимо учитывать ненулевое значение потенциала в нейтральных точках в режиме повреждения.
На рис. 2 показана схема сети по рис. 1, описанная с помощью метода фазных координат.
Рис. 2. Пример схемы с изолированной нейтралью в фазных координатах
Матрицы прямой передачи рассчитываются с помощью уже известных алгоритмов, представленных ранее:
- AЭС для энергосистемы;
- AЛЭП- и AЛЭП+ для линии электропередачи;
- Af для модели повреждения;
- AН для нагрузки.
Схема рис. 2 может быть представлена в виде эквивалентной схемы (рис. 3). Эквивалентная матрица прямой передачи определяется как
Aэкв = AЭС ∙ AЛЭП- ∙ Af ∙ AЛЭП+ ∙ AН.
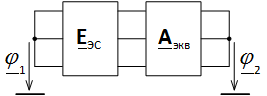
Рис. 3. Эквивалентная схема сети
Для расчёта сети необходимо преобразовать матрицу прямой передачи в матрицу формы Y . Схема преобразованной сети представлена на рис. 4. Там же указаны принятые направления токов, а E1 = EЭС.
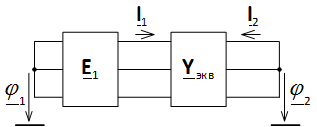
Рис. 4. Схема сети с эквивалентной матрицей формы Y
Для указанной схемы можно записать уравнения
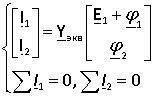
Представим эквивалентную матрицу проводимости в виде
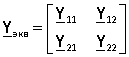
Тогда уравнения схемы можно представить в виде
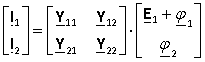
откуда
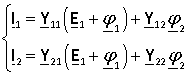
Учитывая, что сумма токов в узлах равна нулю, сложим строки полученных матричных уравнений и упростим уравнения. В итоге получим выражение для расчёта потенциалов точек
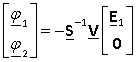
где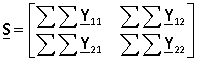 
, 
– сумма всех элементов матрицы Ykj, 
– сумма элементов строк матрицы.
После расчёта потенциалов определяются искомые токи и напряжения.
Расчёт рассматриваемой сети с изолированной нейтралью в среде Matlab приведён в приложенном файле example_isolated_grid.m.
Здравствуйте, если я правильно понял, в результатом работы файла example_isolated_grid.m является массив, три последних элемента которого — это токи Ia, Ib, Ic, соответствующие повреждению. Однако, погонная проводимость ЛЭП равна 0 — линия изолирована от земли, следовательно — это не токи повреждения, а токи обусловленные нагрузкой? Это немного заводит в заблуждение — в начале говорится о расчете КЗ, а в результате получается ток нагрузки. Возможно есть смысл изначально в файле задать не нулевые проводимости линии относительно земли?
Здравствуйте. Да, всё верно, результатом расчёта будут напряжения и токи в месте наблюдения. По поводу расчёта токов КЗ: в данном случае приведён общий расчёт данной схемы, но в приложенном файле с моделью действительно указано только переходное сопротивление в одной фазе. Это не КЗ, а ОЗЗ. Из-за нулевой проводимости это будут просто токи нагрузки. Вы можете поизменять сопротивления других фаз, моделируя различные виды коротких замыканий, при этом будете получать токи КЗ.